题目内容
如图,在△ABC中,点D在AC上,DA=DB,∠C=∠DBC,以AB为直径的 交AC于点E,F是
交AC于点E,F是 上的点,且
上的点,且
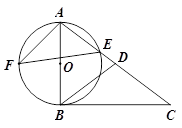
(1)求证:BC是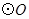 的切线;
的切线;
(2)若sinC=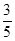 ,AE=
,AE=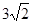 ,求sin∠AFE的值和AF的长.
,求sin∠AFE的值和AF的长.
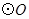 交AC于点E,F是
交AC于点E,F是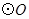 上的点,且
上的点,且 
(1)求证:BC是
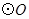 的切线;
的切线; (2)若sinC=
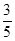 ,AE=
,AE=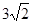 ,求sin∠AFE的值和AF的长.
,求sin∠AFE的值和AF的长.(1)证明见解析(2)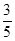 ,5
,5
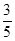 ,5
,5(1)证明:∵DA=DB,
∴∠DAB=∠DBA.
又∵∠C=∠DBC,
∴∠DBA﹢∠DBC= .
.
∴AB⊥BC.
又∵AB是 的直径,
的直径,
∴BC是 的切线.………………………………………………………3分
的切线.………………………………………………………3分
(2)解:如图,连接BE,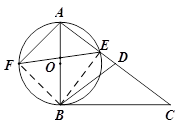
∵AB是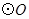 的直径,
的直径,
∴∠AEB=90°.
∴∠EBC+∠C=90°.
∵∠ABC=90°,
∴∠ABE+∠EBC=90°.
∴∠C=∠ABE.
又∵∠AFE=∠ABE,
∴∠AFE=∠C.
∴sin∠AFE=sin∠ABE=sinC.
∴sin∠AFE=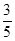 . …………………………………………………………………6分
. …………………………………………………………………6分
连接BF,
∴ .
.
 在Rt△ABE中,
在Rt△ABE中,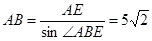 . ……………………………………8分
. ……………………………………8分
∵AF=BF,
∴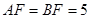 . …………………………………………………………………9分
. …………………………………………………………………9分
(1)欲证BC是⊙O的切线,只需证明∠ABC=90°即可;
(2)如图,连接BE,BF,构建Rt△AEB和Rt△AFB.利用圆周角定理(同弧所对的圆周角相等)、等量代换以及切线的性质推知所求的∠F与已知∠C的数量关系sin∠AFE=sin∠ABE=sinC;然后利用锐角三角函数的定义可以求得sinF的值和AF的长.
∴∠DAB=∠DBA.
又∵∠C=∠DBC,
∴∠DBA﹢∠DBC=
 .
.∴AB⊥BC.
又∵AB是
 的直径,
的直径,∴BC是
 的切线.………………………………………………………3分
的切线.………………………………………………………3分(2)解:如图,连接BE,

∵AB是
 的直径,
的直径,∴∠AEB=90°.
∴∠EBC+∠C=90°.
∵∠ABC=90°,
∴∠ABE+∠EBC=90°.
∴∠C=∠ABE.
又∵∠AFE=∠ABE,
∴∠AFE=∠C.
∴sin∠AFE=sin∠ABE=sinC.
∴sin∠AFE=
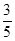 . …………………………………………………………………6分
. …………………………………………………………………6分连接BF,
∴
 .
. 在Rt△ABE中,
在Rt△ABE中,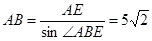 . ……………………………………8分
. ……………………………………8分∵AF=BF,
∴
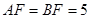 . …………………………………………………………………9分
. …………………………………………………………………9分(1)欲证BC是⊙O的切线,只需证明∠ABC=90°即可;
(2)如图,连接BE,BF,构建Rt△AEB和Rt△AFB.利用圆周角定理(同弧所对的圆周角相等)、等量代换以及切线的性质推知所求的∠F与已知∠C的数量关系sin∠AFE=sin∠ABE=sinC;然后利用锐角三角函数的定义可以求得sinF的值和AF的长.

练习册系列答案
相关题目
 ;
; 的值,其中x是不等式组
的值,其中x是不等式组 的整数解.
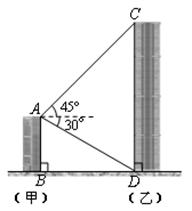
的整数解. ,堤坝高BC=50m,则应水坡面AB的长度是【 】
,堤坝高BC=50m,则应水坡面AB的长度是【 】
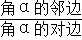 =
=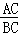 ,根据上述角的余切定义,解下列问题:
,根据上述角的余切定义,解下列问题: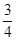 ,其中∠A为锐角,试求ctanA的值.
,其中∠A为锐角,试求ctanA的值.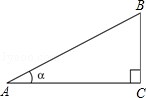
 ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
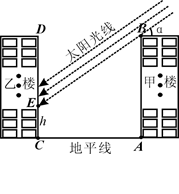

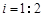 且O,A,B在同一条直线上.求电视塔OC的高度以及此人所在位置P的铅直高度PB.(测倾器高度忽略不计,结果保留根号形式)
且O,A,B在同一条直线上.求电视塔OC的高度以及此人所在位置P的铅直高度PB.(测倾器高度忽略不计,结果保留根号形式) 取1.73).
取1.73).