题目内容
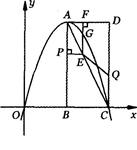
(满分l4分)如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0),C(8,0),D(8,8).抛物线y=ax2+bx过A,C两点.
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于点E,过点E作EF上AD交AD于点F,交抛物线于点G.当t为何值时,线段EG最长?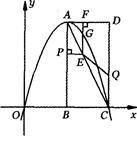
舞:(1)点A的坐标为(4,8). ……3分
将A(4,8),C(8,0)两点坐标分别代人y=ax2+bx, 8=16a+4b,
8=16a+4b,
得
0=64a+8b.
解得a=一 ,b=4.
,b=4.
∴抛物线的解析式为:y=一 x2+4x. ……7分
x2+4x. ……7分
(2)在Rt△APE和Rt△ABC中,tan∠PAE= ,即
,即 =
= =
= ,
,
∴PE= AP=
AP= t,PB=8一t.
t,PB=8一t.
∴点E的坐标为(4+ t,8一t).
t,8一t).
∴点G的纵坐标为:一 (4+
(4+ t) 2+4(4+
t) 2+4(4+ t)=-
t)=- t2+8. ……11分
t2+8. ……11分
∴EG=- t2+8-(8-t)
t2+8-(8-t)
=- t2+t=-
t2+t=- (t-4) 2+2.
(t-4) 2+2.
∵- <0,∴当t=4时,线段EG最长为2. ……14分
<0,∴当t=4时,线段EG最长为2. ……14分
解析

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
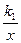 (k1<0,x<0)上一动点,过点P作x轴,y轴的垂线,分别交x轴,y轴于A,B两点,交双曲线y=
(k1<0,x<0)上一动点,过点P作x轴,y轴的垂线,分别交x轴,y轴于A,B两点,交双曲线y=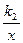 (0<k2<︱k1︱)于E,F两点.
(0<k2<︱k1︱)于E,F两点.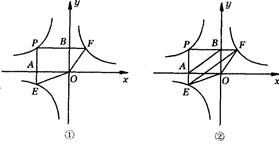
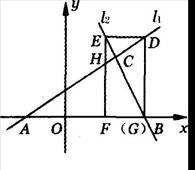
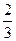 x+
x+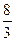 与直线l2:y=2x+16相交于点C,l1,l2分别交x轴于A,B两点.矩形DEFG的顶点D,E分别在直线l1,l2上,顶点F,G都在X轴上,且点G与点B重合.
与直线l2:y=2x+16相交于点C,l1,l2分别交x轴于A,B两点.矩形DEFG的顶点D,E分别在直线l1,l2上,顶点F,G都在X轴上,且点G与点B重合.