题目内容
一个三角形内有n个点,在这些点及三角形顶点之间用线段连接起来,使得这些线段互不相交,且又能把原三角形分割为不重叠的小三角形.如图:若三角形内有1个点时此时有3个小三角形;若三角形内有2个点时,此时有5个小三角形.则当三角形内有3个点时,此时有 个小三角形;当三角形内有n个点时,此时有 个小三角形.


考点:规律型:图形的变化类
专题:
分析:观察图形,不难发现:内部每多一个点,则多2个三角形,则易写出y=3+2(n-1);
解答:解:观察图形发现有如下规律:
∴当三角形内有3个点时,此时有7个小三角形;当三角形内有n个点时,此时有2n+1个小三角形.
故答案为:7,2n+1.
| △ABC内点的个数 | 1 | 2 | 3 | 4 | … | n |
| 分割成的三角形的个数 | 3 | 5 | 7 | 9 | … | 2n+1 |
故答案为:7,2n+1.
点评:此题考查规律型中的图形变化问题,解题关键是结合图形,从特殊推广到一般,建立函数关系式.

练习册系列答案
相关题目
 如图,如果AD∥BC,那么根据
如图,如果AD∥BC,那么根据 如图,直角△DEF是由直角△ABC平移得到的,如果AB=6cm,CF=5cm,DG=2cm,那么图中阴影部分四边形DGCF的面积是
如图,直角△DEF是由直角△ABC平移得到的,如果AB=6cm,CF=5cm,DG=2cm,那么图中阴影部分四边形DGCF的面积是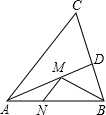 选做题:如图,在锐角△ABC中,AB=2,∠BAC=60°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是
选做题:如图,在锐角△ABC中,AB=2,∠BAC=60°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是