题目内容
已知关于x的方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根;
(2)当抛物线y=kx2+(2k+1)x+2图象与x轴两个交点的横坐标均为整数,且k为正整数时,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2,请结合函数图象确定实数a的取值范围;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,求出定点坐标.
(1)证明:①当k=0时,方程为x+2=0,所以x=﹣2,方程有实数根,
②当k≠0时,∵△=(2k+1)2﹣4k×2=(2k﹣1)2≥0,即△≥0,
∴无论k取任何实数时,方程总有实数根;
(2)解:令y=0,则kx2+(2k+1)x+2=0,
解关于x的一元二次方程,得x1=﹣2,x2=﹣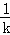 ,
,
∵二次函数的图象与x轴两个交点的横坐标均为整数,且k为正整数,
∴k=1.
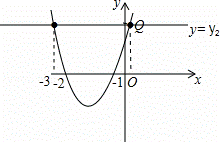
∴该抛物线解析式为y=x2+3x+2,
 .
.
由图象得到:当y1>y2时,a>1或a<﹣3.
(3)依题意得kx2+(2k+1)x+2﹣y=0恒成立,即k(x2+2x)+x﹣y+2=0恒成立,
则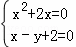 ,
,
解得 或
或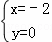 .
.
所以该抛物线恒过定点(0,2)、(﹣2,0).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2秒,方差如表
| 选手 | 甲 | 乙 | 丙 | 丁 |
| 方差(秒2) | 0.020 | 0.019 | 0.021 | 0.022 |
则这四人中发挥最稳定的是( )
|
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
在下列四个图案中,不是中心对称图形的是( )
|
| A. |
| B. |
| C. |
| D. |
|
 的图象经过点
的图象经过点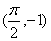 .
. 的最小正周期与单调递增区间.
的最小正周期与单调递增区间.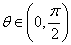 ,且
,且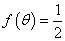 ,求
,求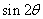 的
的 值.
值. .
.




