题目内容
3．
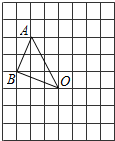如图，在边长为1的小正方形组成的网格中，△AOB的三个顶点均在格点上，点A、B的坐标分别为A（-2，3）、B（-3，1）．（1）画出△AOB绕点O顺时针旋转90°后的△A1OB1；
（2）写出点A1的坐标；
（3）求OB边扫过的面积．
分析 （1）利用网格特点和旋转的性质画出点A、B的对应点A1、B1，则可得到△A1OB1；
（2）根据第一象限点的坐标特征写出点A1的坐标；
（3）OB边扫过的部分为扇形，此扇形的半径为OB，圆心角为90°，然后计算出OB后利用扇形面积公式计算OB边扫过的面积．
解答 解：（1）如图，△A1OB1为所作；
（2）点A1的坐标为（3，2）；
（3）OB=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$，
所以OB边扫过的面积=$\frac{90•π•（\sqrt{10}）^{2}}{360}$=$\frac{5}{2}$π．
点评 旋转图形的作法：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．
练习册系列答案
相关题目
如图，将一副三角板叠放在一起，使直角顶点重合于A，则∠BAC+∠EAD=180°．
15．下列各式中，正确的是（ ）
| A． | $\frac{x^6}{x^2}={x^3}$ | B． | $\frac{x+m}{x+n}=\frac{m}{n}$ | C． | $\frac{-a+b}{c}=-\frac{a+b}{c}$ | D． | $\frac{1}{a}+\frac{1}{b}=\frac{a+b}{ab}$ |
3．
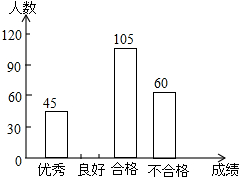为了解今年初二学生的数学学习情况，某校在第一轮模拟测试后，对初二全体同学的数学成绩作了统计分析，绘制如图表：
请结合图表所给出的信息解答下列问题：
（1）该校初二学生共有多少人？
（2）求表中a，b，c的值，并补全条形统计图．
为了解今年初二学生的数学学习情况，某校在第一轮模拟测试后，对初二全体同学的数学成绩作了统计分析，绘制如图表：| 成绩 | 频数 | 频率 |
| 优秀 | 45 | b |
| 良好 | a | 0.3 |
| 合格 | 105 | 0.35 |
| 不合格 | 60 | c |
（1）该校初二学生共有多少人？
（2）求表中a，b，c的值，并补全条形统计图．