题目内容
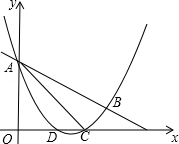
如图,抛物线y= x2+mx+n与直线y=﹣
x2+mx+n与直线y=﹣ x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
(Ⅰ)求抛物线的解析式和tan∠BAC的值;
(Ⅱ)在(Ⅰ)条件下,P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ACB相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
解:(Ⅰ)把A(0,3),C(3,0)代入y= x2+mx+n,得
x2+mx+n,得
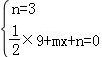 ,解得:
,解得: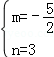 .∴抛物线的解析式为y=
.∴抛物线的解析式为y= x2﹣
x2﹣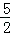 x+3.
x+3.
联立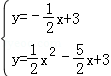 ,解得:
,解得: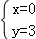 或
或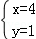 ,∴点B的坐标为(4,1).
,∴点B的坐标为(4,1).
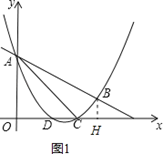
过点B作BH⊥x轴于H,如图1.∵C(3,0),B(4,1),
∴BH=1,OC=3,OH=4,CH=4﹣3=1,∴BH=CH=1.
∵∠BHC=90°,∴∠BCH=45°,BC=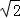 .同理:∠ACO=45°,AC=3
.同理:∠ACO=45°,AC=3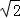 ,
,
∴∠ACB=180°﹣45°﹣45°=90°,∴tan∠BAC=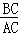 =
=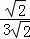 =
= ;
;
(Ⅱ)(1)存在点P,使得以A,P,Q为顶点的三角形与△ACB相似.
过点P作PG⊥y轴于G,则∠PGA=90°.设点P的横坐标为x,由P在y轴右侧可得x>0,则PG=x.
∵PQ⊥PA,∠ACB=90°,∴∠APQ=∠ACB=90°.
若点G在点A的下方,
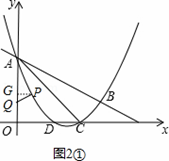
①如图2①,当∠PAQ=∠CAB时,则△PAQ∽△CAB.
∵∠PGA=∠ACB=90°,∠PAQ=∠CAB,∴△PGA∽△BCA,∴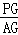 =
=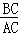 =
= .∴AG=3PG=3x.
.∴AG=3PG=3x.
则P(x,3﹣3x).把P(x,3﹣3x)代入y=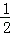 x2﹣
x2﹣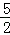 x+3,得:
x+3,得: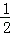 x2﹣
x2﹣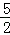 x+3=3﹣3x,
x+3=3﹣3x,
整理得:x2+x=0,解得:x1=0(舍去),x2=﹣1(舍去).
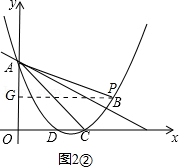
②如图2②,当∠PAQ=∠CBA时,则△PAQ∽△CBA.同理可得:AG=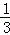 PG=
PG=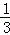 x,则P(x,3﹣
x,则P(x,3﹣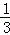 x),
x),
把P(x,3﹣ x)代入y=
x)代入y= x2﹣
x2﹣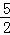 x+3,得:
x+3,得: x2﹣
x2﹣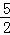 x+3=3﹣
x+3=3﹣ x,
x,
整理得:x2﹣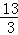 x=0,解得:x1=0(舍去),x2=
x=0,解得:x1=0(舍去),x2=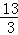 ,∴P(
,∴P(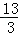 ,
,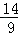 );
);
若点G在点A的上方,
①当∠PAQ=∠CAB时,则△PAQ∽△CAB,
同理可得:点P的坐标为(11,36).
②当∠PAQ=∠CBA时,则△PAQ∽△CBA.
同理可得:点P的坐标为P(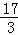 ,
,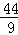 ).
).
综上所述:满足条件的点P的坐标为(11,36)、(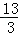 ,
,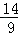 )、(
)、(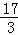 ,
,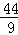 );
);

 初中学业考试导与练系列答案
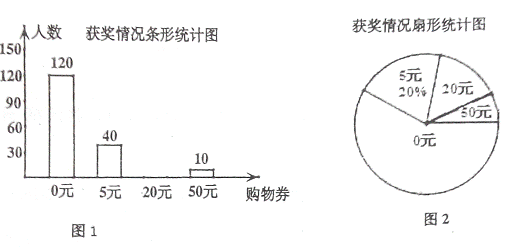
初中学业考试导与练系列答案“五一”期间新华商场贴出促销海报.
甶商场活动期间,小莉同学随机调査了部分 参加活动的顾客
并将调查结果绘制了两幅不完整的统计图.请根据图中信息
解答下列问题:
(1)小莉同学随机调查的顾客有多少人?
(2)补全条形统计图,并求获一等奖的人数占所调查
的人数的百分比是多少?
(3)若商场每天约有2000人次摸奖,请估计商场一天送出的购物券总金额是多少元?
|
 ,则t的值为
,则t的值为 
 ,其中
,其中 ,
, .
. 有意义的
有意义的 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 的值是( )
的值是( )