Question

（2006•河南）如图，山顶建有一座铁塔，塔高BC=80米，测量人员在一个小山坡的P处测得塔的底部B点的仰角为45°，塔顶C点的仰角为60度．已测得小山坡的坡角为30°，坡长MP=40米．求山的高度AB（精确到1米）．（参考数据：≈1.414，≈1.732）

Answer 1

【答案】分析：首先分析图形：根据题意构造直角三角形；本题涉多个直角三角形，应利用其公共边构造关系式，进而可求出答案．
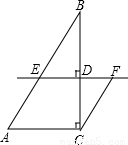
解答：解：如图，过点P作PE⊥AM于E，PF⊥AB于F．
在Rt△PME中，∵∠PME=30°，PM=40，
∴PE=20．∵四边形AEPF是矩形，
∴FA=PE=20．
设BF=x米．∵∠FPB=45°，
∴FP=BF=x．∵∠FPC=60°，
∴CF=PFtan60°=x．∵CB=80，∴80+x=x．
解得x=40（+1}）．
∴AB=40（+1）+20=60+40≈129（米）．
答：山高AB约为129米．
点评：本题要求学生借助俯角构造直角三角形，并结合图形利用三角函数解直角三角形．