题目内容
如图,已知二次函数的图象过点A(0,﹣3),B(![]() ,
,![]() ),对称轴为直线x=﹣
),对称轴为直线x=﹣![]() ,点P是抛物线上的一动点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,在四边形PMON上分别截取PC=
,点P是抛物线上的一动点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,在四边形PMON上分别截取PC=![]() MP,MD=
MP,MD=![]() OM,OE=
OM,OE=![]() ON,NF=
ON,NF=![]() NP.
NP.
(1)求此二次函数的解析式;
(2)求证:以C、D、E、F为顶点的四边形CDEF是平行四边形;
(3)在抛物线上是否存在这样的点P,使四边形CDEF为矩形?若存在,请求出所有符合条件的P点坐标;若不存在,请说明理由.

考点:
二次函数综合题.
分析:
(1)利用顶点式和待定系数法求出抛物线的解析式;
(2)证明△PCF≌△OED,得CF=DE;证明△CDM≌△FEN,得CD=EF.这样四边形CDEF两组对边分别对应相等,所以四边形CDEF是平行四边形;
(3)根据已知条件,利用相似三角形△PCF∽△MDC,可以证明矩形PMON是正方形.这样点P就是抛物线y=x2+x﹣3与坐标象限角平分线y=x或y=﹣x的交点,联立解析式解方程组,分别求出点P的坐标.符合题意的点P有四个,在四个坐标象限内各一个.
解答:
(1)解:设抛物线的解析式为:y=a(x+![]() )2+k,
)2+k,
∵点A(0,﹣3),B(![]() ,
,![]() )在抛物线上,
)在抛物线上,
∴ ,
,
解得:a=1,k=![]() .
.
∴抛物线的解析式为:y=(x+![]() )2
)2![]() =x2+x﹣3.
=x2+x﹣3.
(2)证明:如右图,连接CD、DE、EF、FC.
∵PM⊥x轴于点M,PN⊥y轴于点N,
∴四边形PMON为矩形,
∴PM=ON,PN=OM.
∵PC=![]() MP,OE=
MP,OE=![]() ON,
ON,
∴PC=OE;
∵MD=![]() OM,NF=
OM,NF=![]() NP,
NP,
∴MD=NF,
∴PF=OD.
在△PCF与△OED中,

∴△PCF≌△OED(SAS),
∴CF=DE.
同理可证:△CDM≌△FEN,
∴CD=EF.
∵CF=DE,CD=EF,
∴四边形CDEF是平行四边形.
(3)解:假设存在这样的点P,使四边形CDEF为矩形.
设矩形PMON的边长PM=ON=m,PN=OM=n,则PC=![]() m,MC=
m,MC=![]() m,MD=
m,MD=![]() n,PF=
n,PF=![]() n.
n.
若四边形CDEF为矩形,则∠DCF=90°,易证△PCF∽△MDC,
∴![]() ,即
,即 ,化简得:m2=n2,
,化简得:m2=n2,
∴m=n,即矩形PMON为正方形.
∴点P为抛物线y=x2+x﹣3与坐标象限角平分线y=x或y=﹣x的交点.
联立![]() ,
,
解得 ,
, ,
,
∴P1(![]() ,
,![]() ),P2(﹣
),P2(﹣![]() ,﹣
,﹣![]() );
);
联立![]() ,
,
解得 ,
, ,
,
∴P3(﹣3,3),P4(﹣1,1).
∴抛物线上存在点P,使四边形CDEF为矩形.这样的点有四个,在四个坐标象限内各一个,其坐标分别为:P1(![]() ,
,![]() ),P2(﹣
),P2(﹣![]() ,﹣
,﹣![]() ),P3(﹣3,3),P4(﹣1,1).
),P3(﹣3,3),P4(﹣1,1).

点评:
本题是二次函数综合题型,考查了二次函数的图象与性质、待定系数法、全等三角形、相似三角形、解方程、矩形、正方形等知识点,所涉及的考点较多,但难度均匀,是一道好题.第(2)问的要点是全等三角形的证明,第(3)问的要点是判定四边形PMON必须是正方形,然后列方程组求解.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.
的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C. (2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).
(2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).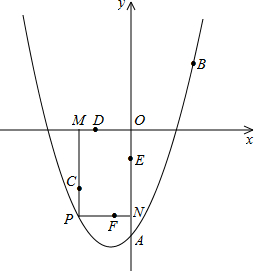 (2013•常德)如图,已知二次函数的图象过点A(0,-3),B(
(2013•常德)如图,已知二次函数的图象过点A(0,-3),B( 如图,已知二次函数的图象与x轴交于A(2,0)、B(6,0)两点,与y轴交于点D(0,4).
如图,已知二次函数的图象与x轴交于A(2,0)、B(6,0)两点,与y轴交于点D(0,4). 如图,已知二次函数的图象(0≤x≤3.4),关于该函数在所给自变量的取值范围内,下列说法正确的是( )
如图,已知二次函数的图象(0≤x≤3.4),关于该函数在所给自变量的取值范围内,下列说法正确的是( )