��Ŀ����
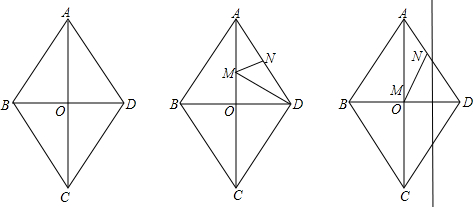
 ��2013•���ң���ͼ�����߳�Ϊ4�ĵȱ�������AOB������ƽ��ֱ������ϵxoy�У�F��AB���ϵĶ��㣨����˵�A��B�غϣ�������F�ķ���������y=
��2013•���ң���ͼ�����߳�Ϊ4�ĵȱ�������AOB������ƽ��ֱ������ϵxoy�У�F��AB���ϵĶ��㣨����˵�A��B�غϣ�������F�ķ���������y=| k |
| x |
��1����S��OCF=
| 3 |
��2���ڣ�1���������£����ж��Ե�EΪԲ�ģ�EA��Ϊ�뾶��Բ��y���λ�ù�ϵ����˵�����ɣ�
��3��AB�����Ƿ���ڵ�F��ʹ��EF��AE�������ڣ������BF��FA��ֵ���������ڣ���˵�����ɣ�
��������1����F��x��y�����õ�OC=x��CF=y����ʾ��������OCF����������xy��ֵ����Ϊk��ֵ������ȷ��������������ʽ��
��2����E��EH��ֱ��x�ᣬEG��ֱ��y�ᣬ��OHΪm�����õȱ������ε����ʼ�������Ǻ��������ʾ��EH��OE��������ʾ��E�����꣬���뷴��������ʽ�����m��ֵ��ȷ����EG��OE��EH�ij�������EA��EG�Ĵ�С��ϵ���ɶ���ԲE��y���λ�ù�ϵ�����жϣ�
��3����E��EH��ֱ��x�ᣬ��FB=x�����õȱ������ε����ʼ�������Ǻ��������ʾ��FC��BC��������ʾ��AF��OC����ʾ��AE��OE�ij����ó�OE��EH�ij�����ʾ��E��F���꣬����E��F���ڷ�����ͼ���ϣ��õ���������˻�����г����̣�������̵Ľ�õ�x��ֵ���������BF��FA�ı�ֵ��
��2����E��EH��ֱ��x�ᣬEG��ֱ��y�ᣬ��OHΪm�����õȱ������ε����ʼ�������Ǻ��������ʾ��EH��OE��������ʾ��E�����꣬���뷴��������ʽ�����m��ֵ��ȷ����EG��OE��EH�ij�������EA��EG�Ĵ�С��ϵ���ɶ���ԲE��y���λ�ù�ϵ�����жϣ�
��3����E��EH��ֱ��x�ᣬ��FB=x�����õȱ������ε����ʼ�������Ǻ��������ʾ��FC��BC��������ʾ��AF��OC����ʾ��AE��OE�ij����ó�OE��EH�ij�����ʾ��E��F���꣬����E��F���ڷ�����ͼ���ϣ��õ���������˻�����г����̣�������̵Ľ�õ�x��ֵ���������BF��FA�ı�ֵ��
����⣺��1����F��x��y������x��0��y��0������OC=x��CF=y��
��S��OCF=
xy=
��
��xy=2
��
��k=2
��
�෴������������ʽΪy=
��x��0����
��2����Բ��y�����룬
����Ϊ������E��EH��x�ᣬ����ΪH������E��EG��y�ᣬ����ΪG��

�ڡ�AOB�У�OA=AB=4����AOB=��ABO=��A=60�㣬
��OH=m����tan��AOB=
=
��
��EH=
m��OE=2m��
��E������m��
m����
��E�ڷ�����y=
ͼ���ϣ�
��
m=
��
��m1=
��m2=-
����ȥ����
��OE=2
��EA=4-2
��EG=
��
��4-2
��
��
��EA��EG��
����EΪԲ�ģ�EA��Ϊ�뾶��Բ��y�����룻
��3�����ڣ�
������ڵ�F��ʹAE��FE��
��E����EH��OB�ڵ�H����BF=x��
�ߡ�AOB�ǵȱ������Σ�
��AB=OA=OB=4����AOB=��ABO=��A=60�㣬

��BC=FB•cos��FBC=
x��FC=FB•sin��FBC=
x��
��AF=4-x��OC=OB-BC=4-
x��
��AE��FE��
��AE=AF•cosA=2-
x��
��OE=OA-AE=
x+2��
��OH=OE•cos��AOB=
x+1��EH=OE•sin��AOB=
x+
��
��E��
x+1��
x+
����F��4-
x��
x����
��E��F����˫����y=
��ͼ���ϣ�
�ࣨ
x+1����
x+
��=��4-
x��•
x��
��ã�x1=4��x2=
��
��BF=4ʱ��AF=0��
�����ڣ���ȥ��
��BF=
ʱ��AF=
��BF��AF=1��4��
��S��OCF=
| 1 |
| 2 |
| 3 |
��xy=2
| 3 |
��k=2
| 3 |
�෴������������ʽΪy=
2
| ||
| x |
��2����Բ��y�����룬
����Ϊ������E��EH��x�ᣬ����ΪH������E��EG��y�ᣬ����ΪG��

�ڡ�AOB�У�OA=AB=4����AOB=��ABO=��A=60�㣬
��OH=m����tan��AOB=
| EH |
| OH |
| 3 |
��EH=
| 3 |
��E������m��
| 3 |
��E�ڷ�����y=
2
| ||
| x |
��
| 3 |
2
| ||
| m |
��m1=
| 2 |
| 2 |
��OE=2
| 2 |
| 2 |
| 2 |
��4-2
| 2 |
| 2 |
��EA��EG��
����EΪԲ�ģ�EA��Ϊ�뾶��Բ��y�����룻
��3�����ڣ�
������ڵ�F��ʹAE��FE��
��E����EH��OB�ڵ�H����BF=x��
�ߡ�AOB�ǵȱ������Σ�
��AB=OA=OB=4����AOB=��ABO=��A=60�㣬

��BC=FB•cos��FBC=
| 1 |
| 2 |
| ||
| 2 |
��AF=4-x��OC=OB-BC=4-
| 1 |
| 2 |
��AE��FE��
��AE=AF•cosA=2-
| 1 |
| 2 |
��OE=OA-AE=
| 1 |
| 2 |
��OH=OE•cos��AOB=
| 1 |
| 4 |
| ||
| 4 |
| 3 |
��E��
| 1 |
| 4 |
| ||
| 4 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
��E��F����˫����y=
| k |
| x |
�ࣨ
| 1 |
| 4 |
| ||
| 4 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
��ã�x1=4��x2=
| 4 |
| 5 |
��BF=4ʱ��AF=0��
| BF |
| AF |
��BF=
| 4 |
| 5 |
| 16 |
| 5 |
�������������ڷ����������ۺ��⣬�漰��֪ʶ�У�������������ͼ�������ʣ�������ͼ�����ʣ��ȱ������ε����ʣ�������Ǻ������壬�������շ�����������ͼ���������ǽⱾ��Ĺؼ���

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
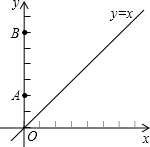 ��2013•���ң���ͼ����ƽ��ֱ������ϵxOy�У�A��0��2����B��0��6��������C��ֱ��y=x�ϣ�����A��B��C����Ϊ������������ǵ��������Σ����C�ĸ����ǣ�������
��2013•���ң���ͼ����ƽ��ֱ������ϵxOy�У�A��0��2����B��0��6��������C��ֱ��y=x�ϣ�����A��B��C����Ϊ������������ǵ��������Σ����C�ĸ����ǣ�������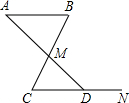 ��2013•���ң���ͼ��AB��CD��BC��AD�ཻ�ڵ�M��N������CD�ϵ�һ�㣮����B=65�㣬��MDN=135�㣬���AMB=
��2013•���ң���ͼ��AB��CD��BC��AD�ཻ�ڵ�M��N������CD�ϵ�һ�㣮����B=65�㣬��MDN=135�㣬���AMB= ��2013•���ң���ͼ���ı���ABCD��ƽ���ı��Σ�E��F�ǶԽ���AC�ϵ����㣬��1=��2��
��2013•���ң���ͼ���ı���ABCD��ƽ���ı��Σ�E��F�ǶԽ���AC�ϵ����㣬��1=��2��