题目内容
如![]() 图,已知在Rt△ABC,AB=AC,∠BAC=90°,过A的任一条直线AN,BD⊥AN于D,CE⊥AN于E
图,已知在Rt△ABC,AB=AC,∠BAC=90°,过A的任一条直线AN,BD⊥AN于D,CE⊥AN于E
⑴求证:DE=BD-CE
⑵如将直线AN绕A点沿顺时针方向旋转,使它不经过△ABC的内部,再作BD⊥AN于D,CE⊥AN于E,那么DE、DB、CE之间还存在等量关系吗?如存在,请证明你的结论?
 |
⑴证明:∵∠BAC=90°,BD⊥AN,∴∠1+∠2=90°,∠1+∠3=90°∴∠2=∠3
∵BD⊥AN,CE⊥AN,∴∠BDA=∠AEC=90°,在△ABD与△CAE中,∠BDA=∠AEC,∠2=∠3,AB=AC,∴△ABD≌△CAE(AAS),∴BD=AE,AD=CE,∵DE=AE-AD,∴DE=BD-CE
⑵证明:如图所示,存在关系式为DE=DB+CE
∵BD⊥AN,CE⊥AN,∴∠BD![]() A=∠CEA=90°,∠1+∠3=90°
A=∠CEA=90°,∠1+∠3=90°
∵∠BAC=90°,∴∠2+∠1=180°-∠BAC=180°-90°=90°
∴∠2=∠3 在△BDA和△AEC中,∠BDA=∠CEA,∠2=∠3,AB=CA,∴△BDA≌△AEC(AAS),∴BD=AE,AD=CE,∴DE=AD+AE=BD+CE


练习册系列答案
相关题目
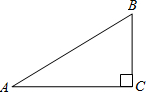 如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为( )
如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为( )| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
 (2012•驿城区模拟)如图,已知在Rt△ABC中,∠B=90°,D、E分别是边AB、AC的中点,若DE=4,AC=10,则AB的值为( )
(2012•驿城区模拟)如图,已知在Rt△ABC中,∠B=90°,D、E分别是边AB、AC的中点,若DE=4,AC=10,则AB的值为( ) 如图,已知在Rt△ABC中,∠C=90°,内切圆的半径为3cm,外接圆的半径为12.5cm,求△ABC的三边长.
如图,已知在Rt△ABC中,∠C=90°,内切圆的半径为3cm,外接圆的半径为12.5cm,求△ABC的三边长. 如图,已知在Rt△ABC中,∠C=90°,点D在BC上,AD=BD,sin∠ADC=
如图,已知在Rt△ABC中,∠C=90°,点D在BC上,AD=BD,sin∠ADC= 如图,已知在Rt△ABC中,∠C=90°.根据要求用尺规作图:
如图,已知在Rt△ABC中,∠C=90°.根据要求用尺规作图: