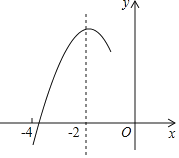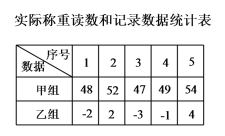Question

【题目】综合与实践

（1）（探索发现）

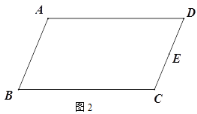
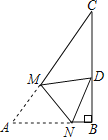
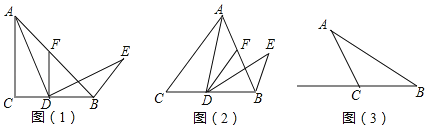
在△ABC中，AC＝BC，∠ACB＝a，点D为直线BC上一动点（点D不与点B，C重合），过点D作DF∥AC交直线AB于点F，将AD绕点D顺时针旋转a得到ED，连接BE，如图（1），当点D在线段BC上，且a＝90°时，试猜想：

①AF与BE之间的数量关系：　 　；

②∠ABE＝　 　．

（2）（拓展探究）

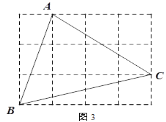
如图（2），当点D在线段BC上，且0°＜a＜90°时，判断AF与BE之间的数量关系及∠ABE的度数，请说明理由．

（3）（解决问题）

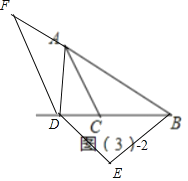
如图（3），在△ABC中，AC＝BC，AB＝4，∠ACB＝a，点D在射线BC上，将AD绕点D顺时针旋转a得到ED，连接BE．当BD＝3CD时，请直接写出BE的长．

Answer 1

【答案】（1）AF＝BF，90°．（2）结论：AF＝BE，∠ABE＝α．（3）2或4．

【解析】

（1）设AB交DE于O，易证△ADF≌△EDB，得到AF＝BE，有因∠DAF＝∠E，∠AOD＝∠EOB，所以∠ABE＝∠ADO＝90°

（2）易证△ADF≌△EDB，得到AF＝BE，∠AFD＝∠EBD，又∠AFD=∠ABC+∠FDB，∠DBE＝∠ABD+∠ABE，所以∠ABE＝∠FDB＝α．

（3）D有可能在BC上，也有可能在BC延长线上，画出图形，利用平行线得到相似，直接利用相似比进行计算即可

解（1）如图1中，设AB交DE于O．

∵∠ACB＝90°，AC＝BC，

∴∠ABC＝45°，

∵DF∥AC，

∴∠FDB＝∠C＝90°，

∴∠DFB＝∠DBF＝45°，

∴DF＝DB，

∵∠ADE＝∠FDB＝90°，

∴∠ADF＝∠EDB，∵DA＝DE，

∴△ADF≌△EDB，

∴AF＝BE，∴∠DAF＝∠E，

∵∠AOD＝∠EOB，

∴∠ABE＝∠ADO＝90°

故答案为AF＝BF，90°．

（2）结论：AF＝BE，∠ABE＝α．理由如下：

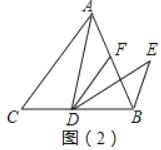
∵DF∥AC

∴∠ACB＝∠FDB＝α，∠CAB＝∠DFB，

∵AC＝BC，

∴∠ABC＝∠CAB，

∴∠ABC＝∠DFB，

∴DB＝DF，

∵∠ADF＝∠ADE﹣∠FDE，∠EDB＝∠FDB﹣∠FDE，

∴∠ADF＝∠EDB，

又∵AD＝DE，

∴△ADF≌△EDB，

∴AF＝BE，∠AFD＝∠EBD

∵∠AFD＝∠ABC+∠FDB，∠DBE＝∠ABD+∠ABE，

∴∠ABE＝∠FDB＝α．

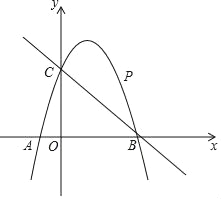
（3）①如图3﹣1中，当点D在BC上时，

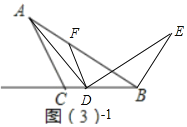
由（2）可知：BE＝AF，

∵DF∥AC，

∴

∵AB＝8，

∴AF＝2，

∴BE＝AF＝2，

②如图3﹣2中，当点D在BC的延长线上时，

∵AC∥DF，

∴

∵AB＝8，

∴AF＝4，

故答案为2或4．