题目内容
如图，已知在⊙O中，如果四边形PBCA内接于圆，且∠BPC=∠CPA=60°，当AB=6时，求BC的长．
解：∵∠BPC，∠BAC为
所对的圆周角，
∴∠BPC=∠BAC，
同理∠CPA=∠CBA，
∵∠BPC=∠CPA=60°，
∴∠BAC=60°，∠CBA=60°，
∴△ABC为等边三角形，
∴AB=BC，
∵AB=6，
∴BC=6．
分析：由同弧所对的圆周角相等求出∠BPC=∠BAC，∠CPA=∠CBA，判断出△ABC为等边三角形，再由等边三角形的性质即可得出结论．
点评：本题考查的是圆周角定理及等边三角形的判定与性质，熟知在同圆或等圆中同弧或等弧所对的圆周角相等是解答此题的关键．
所对的圆周角，∴∠BPC=∠BAC，
同理∠CPA=∠CBA，
∵∠BPC=∠CPA=60°，
∴∠BAC=60°，∠CBA=60°，
∴△ABC为等边三角形，
∴AB=BC，
∵AB=6，
∴BC=6．
分析：由同弧所对的圆周角相等求出∠BPC=∠BAC，∠CPA=∠CBA，判断出△ABC为等边三角形，再由等边三角形的性质即可得出结论．
点评：本题考查的是圆周角定理及等边三角形的判定与性质，熟知在同圆或等圆中同弧或等弧所对的圆周角相等是解答此题的关键．
练习册系列答案
相关题目
20、如图：已知在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E，F．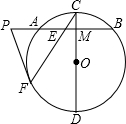
作⊙O的切线交BA的延长线于点P．
（2011•普宁市一模）如图，已知在?ABCD中，E、F是对角线BD延长线上的两点，且∠BCE=∠DAF，求证：△ECD≌△FAB．
如图，已知在△ABC中，AB=AC，AB的垂直平分线DE交AC于点E，CE的垂直平分线正好经过点B，与AC相交于点F，求∠A的度数．