题目内容
20.在四边形ABCD,从下列条件中任取两个组合,使得四边形ABCD是平行四边形的组合有( )种.?①AB∥CD;?②BC∥AD;③?AB=CD;④BC=AD.
| A. | 2组 | B. | 3组 | C. | 4组 | D. | 6组 |
分析 根据平行四边形的判定方法中,①②、③④、①③、②④均可判定是平行四边形.
解答 解:根据平行四边形的判定方法,符合条件的有4种,
分别是:①②、③④、①③、②④.
故选:C.
点评 本题考查了平行四边形的判定,平行四边形的判定方法共有五种,在四边形中如果有:①四边形的两组对边分别平行;②一组对边平行且相等;③两组对边分别相等;④对角线互相平分;⑤两组对角分别相等.则四边形是平行四边形.本题利用了第1,2,3种来判定.

练习册系列答案
相关题目
15.下列条件不能判定两个直角三角形全等的是( )
| A. | 两条直角边对应相等 | B. | 有两条边对应相等 | ||
| C. | 一条边和一个锐角对应相等 | D. | 两个锐角对应相等 |
12.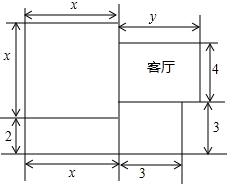 如图是一所住宅的建筑平面图(图中长度单位:m),其中客厅的面积为20m3,这所住宅的建筑面积为S.
如图是一所住宅的建筑平面图(图中长度单位:m),其中客厅的面积为20m3,这所住宅的建筑面积为S.
(1)求y的值,并用含x的式子表示S;
(2)当x=5m时,求S;
(3)当S=x2+41时,求x.
 如图是一所住宅的建筑平面图(图中长度单位:m),其中客厅的面积为20m3,这所住宅的建筑面积为S.
如图是一所住宅的建筑平面图(图中长度单位:m),其中客厅的面积为20m3,这所住宅的建筑面积为S.(1)求y的值,并用含x的式子表示S;
(2)当x=5m时,求S;
(3)当S=x2+41时,求x.
10.已知:a,b互为倒数,m、n互为相反数,x的绝对值是1,则x2-2ab-$\frac{|m+n|}{{x}^{3}}$的值是( )
| A. | -1 | B. | 1 | C. | -2或0 | D. | ±1 |