题目内容
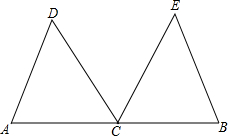 如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.求证:△ACD≌△BCE.
分析:要使△ACD≌△BCE,已知C是线段AB的中点,所以有AC=BC,又因为CD平分∠ACE,CE平分∠BCD,所以∠ACD=∠BCE,故可根据SAS判定两三角形全等.
解答:证明:∵C是线段AB的中点
∴AC=BC
∵CD平分∠ACE,CE平分∠BCD
∴∠ACD=∠ECD,∠BCE=∠ECD
∴∠ACD=∠BCE
在△ACD和△BCE中
∴△ACD≌△BCE(SAS).
∴AC=BC
∵CD平分∠ACE,CE平分∠BCD
∴∠ACD=∠ECD,∠BCE=∠ECD
∴∠ACD=∠BCE
在△ACD和△BCE中
|
∴△ACD≌△BCE(SAS).
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
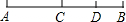 如图,C是线段AB的中点,D是CB上一点,下列说法中错误的是( )
如图,C是线段AB的中点,D是CB上一点,下列说法中错误的是( )| A、CD=AC-BD | ||
B、CD=
| ||
C、CD=
| ||
| D、CD=AD-BC |
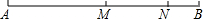

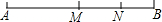 如图,M是线段AB的中点,N是线段MB的中点,且NB=6,求AB的长.
如图,M是线段AB的中点,N是线段MB的中点,且NB=6,求AB的长.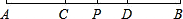 如图,P是线段AB的中点,点C、D把线段AB三等份.已知线段CP的长为2cm,求线段AB的长.
如图,P是线段AB的中点,点C、D把线段AB三等份.已知线段CP的长为2cm,求线段AB的长.