题目内容
【题目】如图,已知抛物线经过点![]() ,
,![]() ,
,![]() 三点.
三点.

![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 若点
若点![]() 是线段
是线段![]() 上的点(不与
上的点(不与![]() ,
,![]() 重合),过
重合),过![]() 作
作![]() 轴交抛物线于
轴交抛物线于![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
![]() 在
在![]() 的条件下,连接
的条件下,连接![]() ,
,![]() ,是否存在点
,是否存在点![]() ,使
,使![]() 的面积最大?若存在,求
的面积最大?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在;当
;(3)存在;当![]() 时,
时,![]() 的面积最大,最大值为
的面积最大,最大值为![]() .
.
【解析】
(1)已知了抛物线上的三个点的坐标,直接利用待定系数法即可求出抛物线的解析式.
(2)先利用待定系数法求出直线BC的解析式,已知点M的横坐标,代入直线BC、抛物线的解析式中,可得到M、N点的坐标,N、M纵坐标的差的绝对值即为MN的长.
(3)设MN交x轴于D,那么△BNC的面积可表示为:S△BNC=S△MNC+S△MNB=![]() MN(OD+DB)=
MN(OD+DB)=![]() MNOB,MN的表达式在(2)中已求得,OB的长易知,由此列出关于S△BNC、m的函数关系式,根据函数的性质即可判断出△BNC是否具有最大值.
MNOB,MN的表达式在(2)中已求得,OB的长易知,由此列出关于S△BNC、m的函数关系式,根据函数的性质即可判断出△BNC是否具有最大值.
![]() 设抛物线的解析式为:
设抛物线的解析式为:![]() ,则:
,则:
![]() ,
,![]() ;
;
∴抛物线的解析式:![]() .
.
![]() 设直线
设直线![]() 的解析式为:
的解析式为:![]() ,则有:
,则有:
![]() ,
,
解得![]() ;
;
故直线![]() 的解析式:
的解析式:![]() .
.
已知点![]() 的横坐标为
的横坐标为![]() ,
,![]() ,则
,则![]() 、
、![]() ;
;
∴故![]() .
.
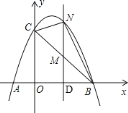
![]() 如图;
如图;
∵![]() ,
,
∴![]() ;
;
∴当![]() 时,
时,![]() 的面积最大,最大值为
的面积最大,最大值为![]() .
.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目