题目内容

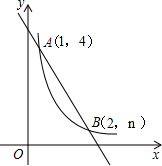如图，一次函数y=kx+b的图象与反比例函数 $数学公式$ 的图象相交于点A（1、4），B（2、n）
（1）求反比例函数和一次函数的表达式；
（2）根据图象回答，当x为何值时，一次函数值大于反比例函数值；
（3）求△AOB的面积；
（4）在第一象限内，双曲线上是否存在一点C，使得△AOC是直角三角形？若存在，求出点C的坐标；若不存在，请说明理由．

解：（1）∵反比例函数 $\text{[math]}$ 的图象经过点A（1，4），B（2，n），
∴4= $\text{[math]}$ ，
解得m=4，
∴反比例函数的解析式为y= $\text{[math]}$ ．
∴n= $\text{[math]}$ ，
∴n=2．
∴B点的坐标为（2，2）．
∵一次函数y=kx+b的图象经过A（1，4），B（2，2），
∴4=k+b，2=2k+b，
解得k=-2，b=6．
∴y=-2x+6；

（2）根据图象可知，当1＜x＜2时，一次函数值大于反比例函数值．

（3）作AE⊥x轴，BF⊥x轴垂足分别为E、F．
则S_△AOB=S_{四边形AEFB}= $\text{[math]}$ （BF+AE）•EF
= $\text{[math]}$ （2+4）×（2-1）
=3；

（4）在第一象限内存在点C，使得△AOC是直角三角形．
理由：设C（a， $\text{[math]}$ ）．
∵OA²=1²+4²=17， $\text{[math]}$ ， $\text{[math]}$ ，
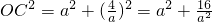（i）显然∠AOC≠90°；
（ii）当∠OAC=90°时，则OA²+AC²=OC²，
∴17+（17+ $\text{[math]}$ = $\text{[math]}$ ，
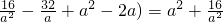，整理，得34- $\text{[math]}$ ，
∴a²-17a+16=0，
（a-16）（a-1）=0，
∴a₁=16，a₂=1．
当a=1时，不合题意，舍去．
∴a=16，则 $\text{[math]}$ ．
∴C（16， $\text{[math]}$ ）；
（iii）当∠ACO=90°时，则AC²+OC²=OA²
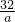
∴（17- 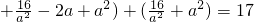$\text{[math]}$ $\text{[math]}$ + $\text{[math]}$ =17，
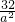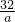整理得 $\text{[math]}$ - $\text{[math]}$ +2a²-2a=0，
32-32a+2a⁴-2a³=0，
32（1-a）-2a³（1-a）=0，
（1-a）（32-2a³）=0，
∴a₁=1， $\text{[math]}$ ，
当a=1时，不合题意舍去．
∴a= $\text{[math]}$ ，
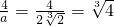∴ $\text{[math]}$ （没有化简，不扣分）
∴C（ $\text{[math]}$ ， $\text{[math]}$ ）．
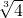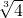综合（i）（ii）（iii）可知当C点的坐标为（16， $\text{[math]}$ ）或（ $\text{[math]}$ ， $\text{[math]}$ ）时，△AOC是直角三角形．
分析：（1）将点A（1、4），B（2、n）分别代入一次函数的解析式y=kx+b与反比例函数 $\text{[math]}$ 的解析式，求出k，b，m即可．
（2）观察图象，可直接得出答案．
（3）作AE⊥x轴，BF⊥x轴垂足分别为E、F，根据反比例函数k的几何意义，可得：S_△AOB=S_{四边形AEFB}即可求解；
（4）设C（a， $\text{[math]}$ ），即可表示出△AOC的三边的长，根据勾股定理的逆定理，分情况讨论，判断m的值，从而确定C的坐标．
点评：本题主要考查了反比例函数中k的几何意义，以及勾股定理的逆定理，注意分情况讨论是关键．