题目内容
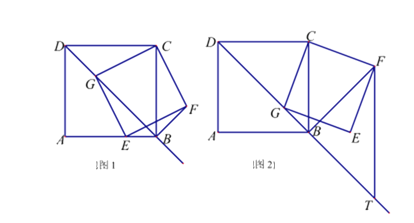
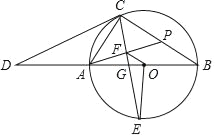
【题目】如图，正方形
的边长为8，
为
上一点，
，
为
边上的一个动点，分别以
为边在正方形内部作等边三角形
和等边三角形
.
(1)证明：
；
(2)直线
与交于点
，点在运动过程中.
①
的度数是否发生改变？若不变，求出这个角的度数；若改变，说明理由；
②连结
，求的最小值.
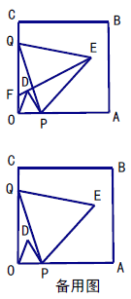
【答案】(1)证明见解析；(2)①不变，
；②
的最小值为5.
【解析】
（1）根据等边三角形的性质，利用三角形全等的判定方法判定
，即可解决；
（2）根据三角形全等的性质，得出∠FOD的度数，利用余角的性质，即可解决；
（3）根据为定值，所以点
的运动路径为线段
，故当
时，的值最小，根据直角三角形中边角关系求解即可.
解：(1)
和
是等边三角形
∴
∴
∴
(2)①
∴
∵
∴
②当点
与点
重合时，以
为边作正三角形
∵为定值，
点的运动路径为线段
过点
作
，垂足为
，
∴当时，的值最小
∵
∴
∴
在
中，
∴
∴
.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
