Question

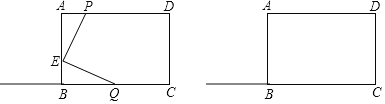
【题目】在长方形ABCD中，长方形ABCD的周长为36厘米，BC比AB大2厘米．点E在线段AB上，且AE=3BE，动点P从A点出发，在线段AD上以每秒1厘米的速度向终点D运动；动点Q从C点出发，沿着射线CB以每秒5厘米的速度运动，三角形APE的面积为S1，三角形EBQ的面积为S2，两点同时出发，当一个点停止运动时，另一个点也停止运动，设它们运动的时间为t秒．

（1）求AB、BC的长；

（2）请用含t的式子分别表示S1和S2；

（3）它们出发几秒时，S1=S2？

Answer 1

【答案】（1）AB=8厘米，BC=10厘米；（2）S1=3t（厘米2），S2=（10﹣5t）（厘米2）；（3）P、Q出发秒或5秒时，S1=S2

【解析】

(1)由矩形的性质得出AB=CD，AD=BC，由题意得出AD=BC=AB+2，由矩形ABCD的周长得出2(AB+BC)=36，求解即可；

(2)由题意得AP=t，CQ=5t，求出BE=2，AE=6，由三角形面积公式得出即可求解；

(3)由题意得出方程3t=10﹣5t或3t=5t﹣10，解方程即可．

(1)∵四边形ABCD是矩形，

∴AB=CD，AD=BC，

由题意得：AD=BC=AB+2，

∵矩形ABCD的周长为36，

∴2(AB+BC)=36，

即2(AB+AB+2)=36，

解得：AB=8，则BC=10，

答：AB=8厘米，BC=10厘米；

(2)由题意得：AP=t，CQ=5t，

∴BQ=10﹣5t，

∵AE=3BE，AB=8，

∴BE=2，AE=6，

∴S1=AE×AP=×6×t=3t(厘米2)，

S2=BE×BQ=×2×(10﹣5t)= （10﹣5t）(厘米2)；

(3)∵S1=S2，

∴3t=10﹣5t或3t=5t﹣10，

解得：t=或t=5，

即P、Q出发秒或5秒时，S1=S2．