题目内容
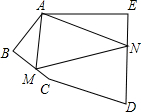 如图,五边形ABCDE中,∠A=120°,∠B=∠E=90°,AB=BC=1,AE=DE=2,在BC、DE上分别找一点M、N,使△AMN的周长最小,则△AMN的周长最小值为
如图,五边形ABCDE中,∠A=120°,∠B=∠E=90°,AB=BC=1,AE=DE=2,在BC、DE上分别找一点M、N,使△AMN的周长最小,则△AMN的周长最小值为
- A.

- B.

- C.

- D.5
B
分析:根据要使△AMN的周长最小,即利用点的对称,让三角形的三边在同一直线上,作出A关于BC和ED的对称点A′,A″,即可得出最短路线,再利用勾股定,求出即可.
解答: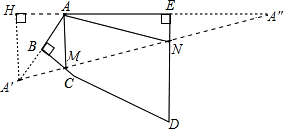 解:作A关于BC和ED的对称点A′,A″,连接A′A″,交BC于M,交ED于N,则A′A″即为△AMN的周长最小值.
解:作A关于BC和ED的对称点A′,A″,连接A′A″,交BC于M,交ED于N,则A′A″即为△AMN的周长最小值.
作EA延长线的垂线,垂足为H,
∵AB=BC=1,AE=DE=2,
∴AA′=2BA=2,AA″=2AE=4,
则Rt△A′HA中,∵∠EAB=120°,∴∠HAA′=60°,
∵A′H⊥HA,
∴∠AA′H=30°,
∴AH= AA′=1,
AA′=1,
∴A′H= =
= ,
,
A″H=1+4=5,
∴A′A″= =2
=2 .
.
故选:B.
点评:此题主要考查了平面内最短路线问题求法以及勾股定理的应用,根据已知得出M,N的位置是解题关键.
分析:根据要使△AMN的周长最小,即利用点的对称,让三角形的三边在同一直线上,作出A关于BC和ED的对称点A′,A″,即可得出最短路线,再利用勾股定,求出即可.
解答:
 解:作A关于BC和ED的对称点A′,A″,连接A′A″,交BC于M,交ED于N,则A′A″即为△AMN的周长最小值.
解:作A关于BC和ED的对称点A′,A″,连接A′A″,交BC于M,交ED于N,则A′A″即为△AMN的周长最小值.作EA延长线的垂线,垂足为H,
∵AB=BC=1,AE=DE=2,
∴AA′=2BA=2,AA″=2AE=4,
则Rt△A′HA中,∵∠EAB=120°,∴∠HAA′=60°,
∵A′H⊥HA,
∴∠AA′H=30°,
∴AH=
 AA′=1,
AA′=1,∴A′H=
 =
= ,
,A″H=1+4=5,
∴A′A″=
 =2
=2 .
.故选:B.
点评:此题主要考查了平面内最短路线问题求法以及勾股定理的应用,根据已知得出M,N的位置是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
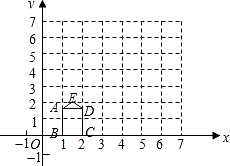 如图,矩形ABCD的长,宽分别为
如图,矩形ABCD的长,宽分别为
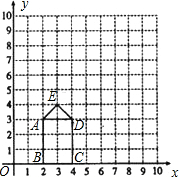 如图,矩形ABCD的长、宽分别为3和2,OB=2,点E的坐标为(3,4)连接AE、ED.
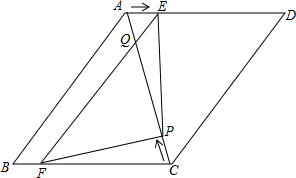
如图,矩形ABCD的长、宽分别为3和2,OB=2,点E的坐标为(3,4)连接AE、ED. 如图,四边形ABCD的内角和为2×180°=360°,五边形ABCDE的内角和为3×180°=540°,…由此可见:
如图,四边形ABCD的内角和为2×180°=360°,五边形ABCDE的内角和为3×180°=540°,…由此可见: