题目内容
【题目】如图，已知点
、
、
、
依次在同一条直线上， 
⊥
于点
， 
⊥
于点
，且
＝
， 
＝
.
（1）求证： 
∥
；
（2）连结
、
，求证： 
＝
.
【答案】（1）证明见解析；（2）证明见解析.
【解析】【试题分析】
（1）根据
＝
，得BF=CE，因为AB=CD,根据两个直角三角形的HL判定定理，得Rt△ABF≌Rt△DCE．根据全等三角形的对应角相等，得∠B=∠C．根据内错角相等，两直线平行，得AB∥DC；
（2）由（1）得：AF=DE,又因为CF=BE, 
,根据SAS，得△AFC≌△DEB．根据群等三角形对应边相等，得AC=BD．
【试题解析】
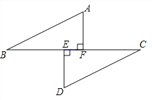
（1）∵AF⊥BC，DE⊥BC，
∴∠DEC=∠AFB=90°．
∵BE=CF，
∴BE+EF=CF+EF．
∴BF=CE．
在Rt△ABF与Rt△DCE中，
∵AB=DC，BF=CE，
∴Rt△ABF≌Rt△DCE．
∴∠B=∠C．
∴AB∥DC．
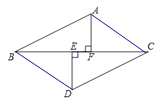
（2）∵Rt△ABF≌Rt△DCE，
∴AF=DE．
∵∠DEB=∠AFC=90°，BE=CF，
∴△AFC≌△DEB．
∴AC=BD．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
