题目内容
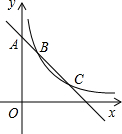 (2012•莆田)如图,一次函数y=k1x+b的图象过点A(0,3),且与反比例函数y=
(2012•莆田)如图,一次函数y=k1x+b的图象过点A(0,3),且与反比例函数y=| k2 | x |
(1)若B(1,2),求k1•k2的值;
(2)若AB=BC,则k1•k2的值是否为定值?若是,请求出该定值;若不是,请说明理由.
分析:(1)分别利用待定系数法求函数解析式求出一次函数解析式与反比例函数解析式,然后代入k1•k2进行计算即可得解;
(2)设出两函数解析式,联立方程组并整理成关于x的一元二次方程,根据AB=BC可知点C的横坐标是点B的横坐标的2倍,再利用根与系数的关系整理得到关于k1、k2的关系式,整理即可得解.
(2)设出两函数解析式,联立方程组并整理成关于x的一元二次方程,根据AB=BC可知点C的横坐标是点B的横坐标的2倍,再利用根与系数的关系整理得到关于k1、k2的关系式,整理即可得解.
解答:解:(1)∵A(0,3),B(1,2)在一次函数y=k1x+b的图象上,
∴
,
解得
;
∵B(1,2)在反比例函数y=
图象上,
∴
=2,
解得k2=2,
所以,k1•k2=(-1)×2=-2;
(2)k1•k2=-2,是定值.
理由如下:∵一次函数的图象过点A(0,3),
∴设一次函数解析式为y=k1x+3,反比例函数解析式为y=
,
∴k1x+3=
,
整理得k1x2+3x-k2=0,
∴x1+x2=-
,x1•x2=-
∵AB=BC,
∴点C的横坐标是点B的横坐标的2倍,不妨设x2=2x1,
∴x1+x2=3x1=-
,x1•x2=2x12=-
,
∴-
=(-
)2,
整理得,k1•k2=-2,是定值.
∴
|
解得
|
∵B(1,2)在反比例函数y=
| k2 |
| x |
∴
| k2 |
| 1 |
解得k2=2,
所以,k1•k2=(-1)×2=-2;
(2)k1•k2=-2,是定值.
理由如下:∵一次函数的图象过点A(0,3),
∴设一次函数解析式为y=k1x+3,反比例函数解析式为y=
| k2 |
| x |
∴k1x+3=
| k2 |
| x |
整理得k1x2+3x-k2=0,
∴x1+x2=-
| 3 |
| k1 |
| k2 |
| k1 |
∵AB=BC,
∴点C的横坐标是点B的横坐标的2倍,不妨设x2=2x1,
∴x1+x2=3x1=-
| 3 |
| k1 |
| k2 |
| k1 |
∴-
| k2 |
| 2k1 |
| 3 |
| 3k1 |
整理得,k1•k2=-2,是定值.
点评:本题是对反比例函数的综合考查,主要利用了待定系数法求函数解析式,根与系数的关系,(2)中根据AB=BC,得到点B、C的坐标的关系从而转化为一元二次方程的根与系数的关系是解题的关键.

练习册系列答案
相关题目
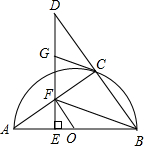 (2012•莆田)如图,点C在以AB为直径的半圆O上,延长BC到点D,使得CD=BC,过点D作DE⊥AB于点E,交AC于点F,点G为DF的中点,连接CG、OF、FB.
(2012•莆田)如图,点C在以AB为直径的半圆O上,延长BC到点D,使得CD=BC,过点D作DE⊥AB于点E,交AC于点F,点G为DF的中点,连接CG、OF、FB. (2012•莆田)如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2012个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
(2012•莆田)如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2012个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( ) (2012•莆田)如图,△A′B′C′是由△ABC沿射线AC方向平移2cm得到,若AC=3cm,则A′C=
(2012•莆田)如图,△A′B′C′是由△ABC沿射线AC方向平移2cm得到,若AC=3cm,则A′C= (2012•莆田)如图,某种新型导弹从地面发射点L处发射,在初始竖直加速飞行阶段,导弹上升的高度y(km)与飞行时间x(s)之间的关系式为
(2012•莆田)如图,某种新型导弹从地面发射点L处发射,在初始竖直加速飞行阶段,导弹上升的高度y(km)与飞行时间x(s)之间的关系式为