题目内容
 (2012•莆田)如图,某种新型导弹从地面发射点L处发射,在初始竖直加速飞行阶段,导弹上升的高度y(km)与飞行时间x(s)之间的关系式为y=
(2012•莆田)如图,某种新型导弹从地面发射点L处发射,在初始竖直加速飞行阶段,导弹上升的高度y(km)与飞行时间x(s)之间的关系式为y=| 1 |
| 18 |
| 1 |
| 6 |
(1)求发射点L与雷达站R之间的距离;
(2)当导弹到达B点时,求雷达站测得的仰角(即∠BRL)的正切值.
分析:(1)在解析式中,把x=3代入函数解析式,即可求得AL的长,在直角△ALR中,利用勾股定理即可求得LR的长;
(2)在解析式中,把x=6代入函数解析式,即可求得AL的长,在直角△BLR中,根据正切函数的定义即可求解.
(2)在解析式中,把x=6代入函数解析式,即可求得AL的长,在直角△BLR中,根据正切函数的定义即可求解.
解答:解:(1)当x=3时,y=
×9+
×3=1(km),
在直角△ALR中,LR=
=
=
(km).
(2)当x=3+3=6时,BL=
×36+
×6=3,
在直角△BLR中,tan∠BRL=
=
=
.
| 1 |
| 18 |
| 1 |
| 6 |
在直角△ALR中,LR=
| AR2-AL2 |
| 22-12 |
| 3 |
(2)当x=3+3=6时,BL=
| 1 |
| 18 |
| 1 |
| 6 |
在直角△BLR中,tan∠BRL=
| BL |
| LR |
| 3 | ||
|
| 3 |
点评:本题是二次函数与三角函数的综合应用,正确求得函数值,理解三角函数的定义是关键.

练习册系列答案
相关题目
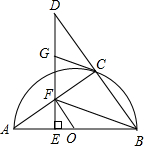 (2012•莆田)如图,点C在以AB为直径的半圆O上,延长BC到点D,使得CD=BC,过点D作DE⊥AB于点E,交AC于点F,点G为DF的中点,连接CG、OF、FB.
(2012•莆田)如图,点C在以AB为直径的半圆O上,延长BC到点D,使得CD=BC,过点D作DE⊥AB于点E,交AC于点F,点G为DF的中点,连接CG、OF、FB. (2012•莆田)如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2012个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
(2012•莆田)如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2012个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( ) (2012•莆田)如图,△A′B′C′是由△ABC沿射线AC方向平移2cm得到,若AC=3cm,则A′C=
(2012•莆田)如图,△A′B′C′是由△ABC沿射线AC方向平移2cm得到,若AC=3cm,则A′C=