题目内容
从1开始,连续的自然数相加,它们的和的倒数情况如下表:
(1)根据表中规律,求 =______;
=______;
(2)根据表中规律,则 =______;
=______;
(3)求 +
+ +
+ +
+ 的值.
的值.
| 分母中加数的个数 | 和的倒数 |
| 2 |  |
| 3 |  |
| 4 |  |
| 5 |  |
| … | … |
解:(1)按照下表的规律,可以 =2(
=2( -
- )=
)=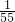 ;
;
(2)根据表中规律,则 =
=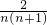 ;
;
(3)由表中几个式子我们可以得出规律,即 =
=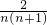 =
=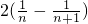 .所以
.所以 +
+ +
+ +
+ =2(
=2( +…
+… )=2(
)=2(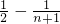 )=
)=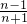 ;
;
分析:根据上图的几个例子我们可以总结出规律,即根据表中规律,则 =
=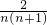 =
=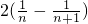 .
.
点评:本题属于找规律的题目,另外还需要学生对规律的灵活应用.
 =2(
=2( -
- )=
)=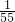 ;
;(2)根据表中规律,则
 =
=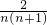 ;
;(3)由表中几个式子我们可以得出规律,即
 =
=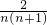 =
=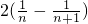 .所以
.所以 +
+ +
+ +
+ =2(
=2( +…
+… )=2(
)=2(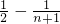 )=
)=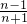 ;
;分析:根据上图的几个例子我们可以总结出规律,即根据表中规律,则
 =
=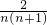 =
=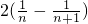 .
.点评:本题属于找规律的题目,另外还需要学生对规律的灵活应用.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
从1开始,连续的自然数相加,它们的和的倒数情况如下表:
(1)根据表中规律,求
= ;
(2)根据表中规律,则
= ;
(3)求
+
+
+
的值.
(1)根据表中规律,求
| 1 |
| 1+2+3+…+10 |
(2)根据表中规律,则
| 1 |
| 1+2+3+4+…+n |
(3)求
| 1 |
| 1+2 |
| 1 |
| 1+2+3 |
| 1 |
| 1+2+3+4 |
| 1 |
| 1+2+3+4+…+n |
| 分母中加数的个数 | 和的倒数 | ||||||||
| 2 |
| ||||||||
| 3 |
| ||||||||
| 4 |
| ||||||||
| 5 |
| ||||||||
| … | … |