题目内容
 为改善市区人民生活环境,市建设污水管网工程,截面如图.若管内污水的面宽AB=40cm,污水的最大深度为10cm,则圆柱型水管的直径为
为改善市区人民生活环境,市建设污水管网工程,截面如图.若管内污水的面宽AB=40cm,污水的最大深度为10cm,则圆柱型水管的直径为考点:垂径定理的应用,勾股定理
专题:
分析:首先连接OA,过点O作OE⊥AB,交⊙O于F,根据垂径定理,即可求得AE的值,然后在Rt△OAE中,利用勾股定理,即可求得OA的值,进而得出答案.
解答: 解:连接OA,过点O作OE⊥AB,交⊙O于F,
解:连接OA,过点O作OE⊥AB,交⊙O于F,
∵管内污水的面宽AB=40cm,污水的最大深度为10cm,
∴AE=20cm,EF=10cm,
设AO=xcm,则EO=(x-10)cm,
在Rt△AOE中,
AO2=EO2+AE2,
则x2=(x-10)2+202,
解得:x=25,
故圆柱型水管的直径为50cm.
故答案为:50.
 解:连接OA,过点O作OE⊥AB,交⊙O于F,
解:连接OA,过点O作OE⊥AB,交⊙O于F,∵管内污水的面宽AB=40cm,污水的最大深度为10cm,
∴AE=20cm,EF=10cm,
设AO=xcm,则EO=(x-10)cm,
在Rt△AOE中,
AO2=EO2+AE2,
则x2=(x-10)2+202,
解得:x=25,
故圆柱型水管的直径为50cm.
故答案为:50.
点评:此题主要考查了勾股定理和垂径定理的应用,此类题要构造一个由半径、半弦、弦心距组成的直角三角形,然后根据勾股定理以及垂径定理进行计算.

练习册系列答案
相关题目
在实数
、
、(
)2、
、π中,无理数有( )个.
| 3 | 4 |
| 8 |
| 2 |
| 23 |
| 7 |
| A、1 | B、2 | C、3 | D、4 |
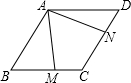 如图,在?ABCD中,∠ABC=60°,且AB=BC,∠MAN=60°,请探索BM,DN与AB的数量关系,并证明你的结论.
如图,在?ABCD中,∠ABC=60°,且AB=BC,∠MAN=60°,请探索BM,DN与AB的数量关系,并证明你的结论. 如图,正方形ABCD中,AC=AF,AF交CD于E,DF∥AC.求证:CF=CE.
如图,正方形ABCD中,AC=AF,AF交CD于E,DF∥AC.求证:CF=CE.