题目内容
如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.

(1)求C点坐标;
(2)求直线MN的解析式;
(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
(1)C(0,6)。
(2)y= x+6。
x+6。
(3)P1(4,3),P2( )P3(
)P3( ),P4(
),P4( )。
)。
【解析】
试题分析:(1)通过解方程x2﹣14x+48=0可以求得OC=6,OA=8.则C(0,6)。
解方程x2﹣14x+48=0得x1=6,x2=8。
∵OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根,
∴OC=6,OA=8.∴C(0,6)。
(2)设直线MN的解析式是y=kx+b(k≠0),把点A、C的坐标分别代入解析式,列出关于系数k、b的方程组,通过解方程组即可求得它们的值。
设直线MN的解析式是y=kx+b(k≠0),
由(1)知,OA=8,则A(8,0)。
∵点A、C都在直线MN上,
∴ ,解得
,解得 。
。
∴直线MN的解析式为y= x+6。
x+6。
(3)需要分类讨论:PB为腰,PB为底两种情况下的点P的坐标.根据等腰三角形的性质、勾股定理以及一次函数图象上点的坐标特征进行解答:

∵A(8,0),C(0,6),∴根据题意知B(8,6)。
∵点P在直线MN:y= x+6上,∴设P(a,
x+6上,∴设P(a, a+6)。
a+6)。
当以点P,B,C三点为顶点的三角形是等腰三角形时,需要分类讨论:
①当PC=PB时,点P是线段BC的中垂线与直线MN的交点,则P1(4,3)。
②当PC=BC时,a2+( a+6﹣6)2=64,解得,a=
a+6﹣6)2=64,解得,a= ,则P2(
,则P2( ),P3(
),P3( )。
)。
③当PB=BC时,(a﹣8)2+( a+6﹣6)2=64,解得,a=
a+6﹣6)2=64,解得,a= ,则P4(
,则P4( )。
)。
综上所述,符合条件的点P有:P1(4,3),P2( )P3(
)P3( ),P4(
),P4( )。
)。

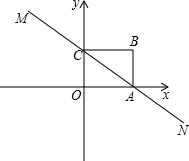 (2013•绥化)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根.
(2013•绥化)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根. 如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根.
如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根.
