题目内容
如图，△ABC中，以B为圆心，BC长为半径画弧，分别交AC、AB于D，E两点，并连接BD，DE．若∠A=30°，AB=AC，则∠BDE的度数为何（ ）
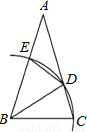
A．45 B．52.5 C．67.5 D．75
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
如图，△ABC中，以B为圆心，BC长为半径画弧，分别交AC、AB于D，E两点，并连接BD，DE．若∠A=30°，AB=AC，则∠BDE的度数为何（ ）
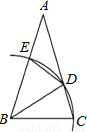
A．45 B．52.5 C．67.5 D．75
阅读快车系列答案
轴交于A（
，0）、B（
，0）两点，且
，与
轴交于点
，其中
,
是方程
的两个根。
