题目内容
把一个长方形（如图）划分成两个全等的长方形．若要使每一个小长方形与原长方形相似，问原长方形应满足什么条件？分析：设AE=ED=a，AB=b，根据每一个小长方形与原长方形相似，可知
=
，再由a，b均为正数可知b=
a，故
=
=
=
，由此即可得出结论．
| a |
| b |
| b |
| 2b |
| 2 |
| AD |
| AB |
| 2a |
| b |
| 2a | ||
|
| 2 |
解答：解：设AE=ED=a，AB=b，
∵每一个小长方形与原长方形相似，
∴
=
，
∴b2=2a2，
∵a，b均为正数，∴b=
a，
∴
=
=
=
，
∴原长方形的长与宽之比为
：1．
∵每一个小长方形与原长方形相似，
∴
| a |
| b |
| b |
| 2a |
∴b2=2a2，
∵a，b均为正数，∴b=
| 2 |
∴
| AD |
| AB |
| 2a |
| b |
| 2a | ||
|
| 2 |
∴原长方形的长与宽之比为
| 2 |
点评：本题考查的相似多边形的性质，即相似多边形对应边的比叫做相似比．
练习册系列答案
相关题目
把一个长方形分成如图所示由完全一样的7个小长方形拼成的大长方形，且这7个小长方形能完全重合．已知大长方形的宽为14cm，设小长方形的宽为xcm，则可列方程为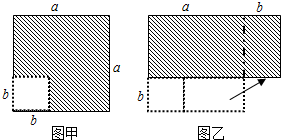
探索与应用
把一个长方形分成如图所示由完全一样的7个小长方形拼成的大长方形，且这7个小长方形能完全重合．已知大长方形的宽为14cm，设小长方形的宽为xcm，则可列方程为________．
把一个长方形（如图）划分成两个全等的长方形．若要使每一个小长方形与原长方形相似，问原长方形应满足什么条件？