题目内容
当0＜a＜1时，把a，
，a2用“＜”排列起来是
| 1 |
| a |
a2＜a＜
| 1 |
| a |
a2＜a＜
．| 1 |
| a |
分析：此题中的有理数比较复杂，故可用特殊值法求解，假设a=
，则
=2，a2=
，再比较出其大小即可．
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| 4 |
解答：解：假设a=
，则
=2，a2=
，
∵
＜
＜2，
∴a2＜a＜
．
故答案为：a2＜a＜
．
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| 4 |
∵
| 1 |
| 4 |
| 1 |
| 2 |
∴a2＜a＜
| 1 |
| a |
故答案为：a2＜a＜
| 1 |
| a |
点评：本题考查的是有理数的大小比较，在解答此类问题时要注意特殊值法的应用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
为了探究n条直线能把平面最多分成几部分，我们从最简单的情形入手．
（1）一条直线把平面分成2部分；
（2）两条直线最多可把平面分成4部分；
（3）三条直线最多可把平面分成11部分…；
把上述探究的结果进行整理，列表分析：
（1）当直线条数为5时，把平面最多分成 部分，写成和的形式 ；
（2）当直线为10条时，把平面最多分成 部分；
（3）当直线为n条时，把平面最多分成 部分．（不必说明理由）
（1）一条直线把平面分成2部分；
（2）两条直线最多可把平面分成4部分；
（3）三条直线最多可把平面分成11部分…；
把上述探究的结果进行整理，列表分析：
| 直线条数 | 把平面分成部分数 | 写成和形式 |
| 1 | 2 | 1+1 |
| 2 | 4 | 1+1+2 |
| 3 | 7 | 1+1+2+3 |
| 4 | 11 | 1+1+2+3+4 |
| … | … | … |
（2）当直线为10条时，把平面最多分成
（3）当直线为n条时，把平面最多分成
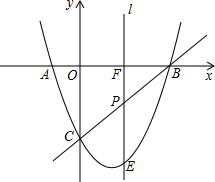点C．点P为线段BC上一点，过点P作直线l⊥x轴于点F，交抛物线c1点E．
