题目内容
 如图,一艘海轮在A点时测得灯塔C在它的北偏东42°方向上,它沿正东方向航行80海里后到达B处,此时灯塔C在它的北偏西55°方向上.
如图,一艘海轮在A点时测得灯塔C在它的北偏东42°方向上,它沿正东方向航行80海里后到达B处,此时灯塔C在它的北偏西55°方向上.(1)求海轮在航行过程中与灯塔C的最短距离(结果精确到0.1);
(2)求海轮在B处时与灯塔C的距离(结果保留整数).
(参考数据:sin55°≈0.819,cos55°≈0.574,tan55°≈1.428,tan42°≈0.900,tan35°≈0.700,tan48°≈1.111)
考点:解直角三角形的应用-方向角问题
专题:几何图形问题
分析:(1)过C作AB的垂线,设垂足为D,则CD的长为海轮在航行过程中与灯塔C的最短距离;
(2)在Rt△BCD中,根据55°角的余弦值即可求出海轮在B处时与灯塔C的距离.
(2)在Rt△BCD中,根据55°角的余弦值即可求出海轮在B处时与灯塔C的距离.
解答: 解:(1)过C作AB的垂线,设垂足为D,
解:(1)过C作AB的垂线,设垂足为D,
根据题意可得:∠1=∠2=42°,∠3=∠4=55°,
设CD的长为x海里,
在Rt△ACD中,tan42°=
,则AD=x•tan42°,
在Rt△BCD中,tan55°=
,则BD=x•tan55°,
∵AB=80,
∴AD+BD=80,
∴x•tan42°+x•tan55°=80,
解得:x≈34.4,
答:海轮在航行过程中与灯塔C的最短距离是34.4海里;
(2)在Rt△BCD中,cos55°=
,
∴BC=
≈60海里,
答:海轮在B处时与灯塔C的距离约为60海里.
 解:(1)过C作AB的垂线,设垂足为D,
解:(1)过C作AB的垂线,设垂足为D,根据题意可得:∠1=∠2=42°,∠3=∠4=55°,
设CD的长为x海里,
在Rt△ACD中,tan42°=
| AD |
| CD |
在Rt△BCD中,tan55°=
| BD |
| CD |
∵AB=80,
∴AD+BD=80,
∴x•tan42°+x•tan55°=80,
解得:x≈34.4,
答:海轮在航行过程中与灯塔C的最短距离是34.4海里;
(2)在Rt△BCD中,cos55°=
| CD |
| BC |
∴BC=
| CD |
| cos55° |
答:海轮在B处时与灯塔C的距离约为60海里.
点评:本题考查了解直角三角形的应用:方向角问题,具体就是在某点作出东南西北,即可转化角度,也得到垂直的直线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知实数a,b,若a>b.则正确的是( )
| A、a-5<b-5 | ||||
| B、2+a<2+b | ||||
C、
| ||||
| D、-2a<-2b |
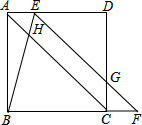 如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H,AE=CF,BE=EG.
如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H,AE=CF,BE=EG. 如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).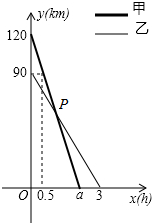 在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题:
在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题: