题目内容
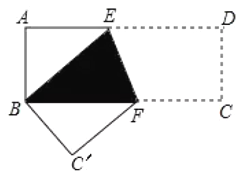
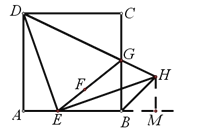
【题目】如图，在正方形ABCD中，E是边AB上的任意一点(不与点A，B重合)，连接DE，作点A关于直线DE的对称点为F，连接EF并延长交BC于点G．
（1）依题意补全图形，连接DG，求∠EDG的度数；
（2）过点E作EH⊥DE交DG的延长线于点H，连接BH．线段BH与AE有怎样的数量关系，请写出结论并证明．
【答案】（1）作图见解析，45°；（2）
，证明见解析．
【解析】
（1）根据题目的已知，作图即可；连接
，根据对称得：
，再由
证明
，可得结论；
（2）过点H作
的延长线于点M，根据
得到
，
由（1）得：
，则
，可证
≌
，则有
，可得
，即
是等腰直角三角形，可证得．
（1）补全的图形，如图所示．
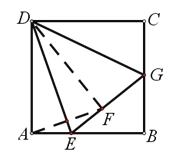
连接DF
∵四边形ABCD是正方形，
∴
，
∵点
为点
关于
的对称点，
∴≌
．
∴
，
∴
．
又∵
，
∴
≌
（HL）
∴
，
∴
．
（2）如图所示．
线段BH与AE的数量关系为
如图，过点H作的延长线于点M，
，∴，
∴
由（1）得：∴
∴
∴≌
∴
，
∴
是等腰直角三角形，
∴．
练习册系列答案
阅读快车系列答案
相关题目
