题目内容

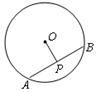
如图，点P是半径为5的⊙O内的一点，且OP＝3，设AB是过点P的 ⊙O内的弦，且AB⊥OP，则弦AB长是________．
8

试题分析：如图，点P是半径为5的⊙O内的一点，且OP＝3，设AB是过点P的 ⊙O内的弦，且AB⊥OP，根据弦的性质，AP=BP，AB=2AP；在直角三角形AOP中，由勾股定理可得AP=，所以AB=8
点评：本题考查弦，解答本题的关键是掌握圆中弦的性质，熟悉勾股定理的内容，本题属基础题
练习册系列答案
相关题目
如图，在△ABC中，AB=AC，点O在边AB上，⊙O过点B且分别与边AB、BC相交于点D、E，EF⊥AC，垂足为F．求证：直线EF是⊙O的切线．
如图，四边形ABCD是平行四边形，以对角线BD为直径作⊙O，分别于BC、AD相交于点E、F.

（1）求证四边形BEDF为矩形.
（2）若BD2=BE·BC，试判断直线CD与⊙O的位置关系，并说明理由.
如图，AB是⊙O的直径，点C在⊙O上，弦BD平分∠ABC，则下列结论错误的是
A．AD=DCB．C．∠ADB=∠ACBD．∠DAB=∠CBA
若⊙A和⊙B相切，它们的半径分别为8cm和2cm，则圆心距AB为
　   　cm．
如图，直线AB与⊙O相切于点A，AC、CD是⊙O的两条弦，且CD∥AB，若⊙O 的半径为，CD=4，则弦AC的长为     ．
如图，点A、B在⊙O上，直线AC是⊙O的切线，OC⊥OB，连接AB交OC于点D．

（1）AC与CD相等吗？为什么？
（2）若AC=2，AO=，求OD的长度．
如图，已知△ABC为等腰直角三角形，D为斜边BC的中点，经过点A、D的⊙O与△ABC三边分别交于点E、F、M．对于如下四个结论：①∠EMB=∠FMC；②AE+AF＝AC；③△DEF∽△ABC；④四边形AEMF是矩形．其中正确结论的个数是

A.4        B.3             C.2              D.1
若两圆的圆心距为，两圆的半径分别是方程的两个根，则两圆的位置关系是_____．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网