��Ŀ����
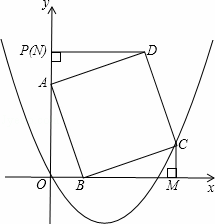
��ͼ����ƽ��ֱ������ϵ�У���֪��P��0��4������A���߶�OP�ϣ���B��x���������ϣ���AP=OB=t�� 0��t��4����ABΪ���ڵ�һ��������������ABCD������C��D������x�ᡢy�������ߣ�����ΪM��N�����O��C�����������Ϊy=ax2+bx+c��
0��t��4����ABΪ���ڵ�һ��������������ABCD������C��D������x�ᡢy�������ߣ�����ΪM��N�����O��C�����������Ϊy=ax2+bx+c��
��1����գ���AOB�ա��� ���ա�BMC������֤�������ú�t�Ĵ���ʽ��ʾA�������꣺A��0���� ������
��2�����C�����꣬���ú�a��t�Ĵ���ʽ��ʾb��
��3����t=1ʱ������OD������ʱ���������߶�ODֻ��Ψһ�Ĺ�����O����a��ȡֵ��Χ��
��4���������߿������ϣ��Գ�����ֱ��x=2﹣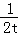 ���������ŵ����������ƶ�ʱ����t��ȡֵ��Χ��
���������ŵ����������ƶ�ʱ����t��ȡֵ��Χ��
�⣺��1����ͼ���ߡ�DNA=��AOB=90�㣬
���NAD=��OBA��ͬ�ǵ������ȣ���
�ڡ�AOB���DNA�У� ��
��
���AOB�ա�DNA��SAS����
ͬ����DNA�ա�BMC��
�ߵ�P��0��4����AP=t��
��OA=OP﹣AP=4﹣t��
�ʴ��ǣ�DNA���DPA��4﹣t��
��2��������֪��NA=OB=t����OA=4﹣t��
�ߡ�AOB�ա�BMC��
��CM=OB=t��
��OM=OB+BM=t+4﹣t=4��
��C��4��t����
��������y=ax2+bx+c����O��C��
�� ��
��
��� b= t﹣4a��
t﹣4a��
��3����t=1ʱ��������Ϊy=ax2+�� ﹣4a��x��NA=O
﹣4a��x��NA=O B=1��OA=3��
B=1��OA=3��
�ߡ�AOB�ա�DNA��
��DN=OA=3��
��D��3��4����
��ֱ��ODΪ��y=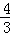 x��
x��
���������飬�� ��
��
��ȥy����
ax2+��﹣ ﹣4a��x=0��
﹣4a��x=0��
��� x=0��x=4+ ��
��
���ԣ���������ֱ��OD�����������㣮
���ۣ��ٵ�a��0ʱ��4+ ��3��ֻ�н���O������a��0�������⣻
��3��ֻ�н���O������a��0�������⣻
�ڵ�a��0ʱ����4+ ��3����a��﹣
��3����a��﹣ ��
��
��a��0
���� a��﹣ ��
��
��4+ ��0�����a��﹣
��0�����a��﹣ ��
��
��a��0��
����﹣ ��a��0��
��a��0��
����������a��ȡֵ��Χ��a��0��a��﹣ ��﹣
��﹣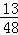 ��a��0��
��a��0��
��4��������Ϊy=ax2+�� ﹣4a��x���������ǣ�﹣
﹣4a��x���������ǣ�﹣ ��﹣
��﹣ ��t﹣16a��2����
��t﹣16a��2����
�֡߶Գ�����ֱ��x=﹣ +2=2﹣
+2=2﹣ ��
��
��a= t2��
t2��
�ඥ������Ϊ����2﹣ ��﹣
��﹣ ��1﹣4t��2��������2﹣
��1﹣4t��2��������2﹣ ��﹣��t﹣
��﹣��t﹣ ��2����
��2����
�������߿������ϣ�������t�����������ߵĶ��������ƶ���
��ֻ�붥�������йأ�
��t��ȡֵ��ΧΪ��0��t�� ��
��
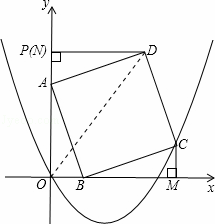

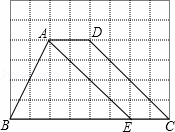
��ͼ����A��B��C��D���ڡ�O�ϣ�AC��BD�ཻ�ڵ�E�����ABD=��������
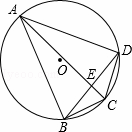
| �� | A�� | ��ACD | B�� | ��ADB | C�� | ��AED | D�� | ��ACB |
�±��У�y��x��һ�κ�����
| x | ﹣2 | 1 | 2 | ��4�� | 5 |
| y | 6 | ﹣3 | ��﹣6�� | ﹣12 | ﹣15 |
��1����ú����ı���ʽ������ȫ����
��2����֪�ú���ͼ����һ��M��1��﹣3��Ҳ�ڷ���������y=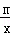 ͼ���ϣ�������������ͼ�����һ����N�����꣮
ͼ���ϣ�������������ͼ�����һ����N�����꣮
�Բμ�ij��Ұ��ѵ������ѧ�������䣨��λ���꣩����ͳ�ƣ���������
| ���� | 13 | 14 | 15 | 16 | 17 | 18 |
| ���� | 4 | 5 | 6 | 6 | 7 | 2 |
����Щѧ���������������λ���ֱ��ǣ�������
| �� | A�� | 17��15.5 | B�� | 17��16 | C�� | 15��15.5 | D�� | 16��16 |
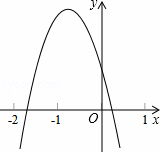
��֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ�����н��ۣ�
��abc��0����2a��b��0����4a��2b+c��0���ܣ�a+c��2��b2
������ȷ�ĸ����У�������
| �� | A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
��ʽ�ֽ�a2b��b����ȷ����ǣ�������
| �� | A�� | b��a+1����a��1�� | B�� | a��b+1����b��1�� | C�� | b��a2��1�� | D�� | b��a��1��2 |
 ��x��0����ͼ����A����1��1��������A��AB��y�ᣬ����ΪB����y�����������ȡһ��P��0��t��������P��ֱ��OA�Ĵ���l����ֱ��lΪ�Գ��ᣬ��B����ԳƱ任�õ��ĵ�B���ڴ˷�����������ͼ���ϣ���t��ֵ�ǣ�������
��x��0����ͼ����A����1��1��������A��AB��y�ᣬ����ΪB����y�����������ȡһ��P��0��t��������P��ֱ��OA�Ĵ���l����ֱ��lΪ�Գ��ᣬ��B����ԳƱ任�õ��ĵ�B���ڴ˷�����������ͼ���ϣ���t��ֵ�ǣ�������
 B��
B��  C��
C��  D��
D��