题目内容
2.计算:($\sqrt{3}+\sqrt{2}-1$)($\sqrt{3}-\sqrt{2}+1$)=( )| A. | -2$\sqrt{2}$ | B. | 4+2$\sqrt{3}$ | C. | 4-2$\sqrt{3}$ | D. | 2$\sqrt{2}$ |
分析 直接利用平方差公式计算,进而结合完全平方公式求出答案.
解答 解:($\sqrt{3}+\sqrt{2}-1$)($\sqrt{3}-\sqrt{2}+1$)
=[$\sqrt{3}$+($\sqrt{2}$-1)][$\sqrt{3}$-($\sqrt{2}$-1)]
=3-($\sqrt{2}$-1)2
=3-(3-2$\sqrt{2}$)
=2$\sqrt{2}$.
故选:D.
点评 此题主要考查了二次根式的混合运算,正确应用乘法公式是解题关键.

练习册系列答案
相关题目
12.若m=2+$\sqrt{3}$,n=2-$\sqrt{3}$,则m2013•n2014的值为( )
| A. | 1 | B. | -1 | C. | 2-$\sqrt{3}$ | D. | $\sqrt{3}-2$ |
17.下列计算正确的是( )
| A. | $\sqrt{(-4)^2}$=-4 | B. | ($\sqrt{2}$)2=4 | C. | $\sqrt{5}$+$\sqrt{2}$=$\sqrt{7}$ | D. | $\sqrt{18}$÷$\sqrt{2}$=3 |
7.|-9|的值是( )
| A. | 9 | B. | -9 | C. | $\frac{1}{9}$ | D. | -$\frac{1}{9}$ |
11.下面给出了6个式子:
①3>0;②4x+3y>0;③x=3;④x-1;⑤x+2≤3;⑥2x≠0.
其中不等式有( )
①3>0;②4x+3y>0;③x=3;④x-1;⑤x+2≤3;⑥2x≠0.
其中不等式有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
12.己知反比例函数y=$\frac{6}{x}$,当1<x<3时,y的取值范围是( )
| A. | 0<y<l | B. | 1<y<2 | C. | y>6 | D. | 2<y<6 |
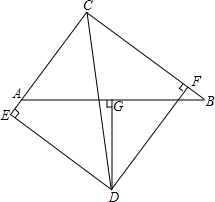 已知:如图,△ABC中,AC=6,BC=8,AB=10,∠BCA的平分线与AB边的垂直平分线相交于点D,DE⊥AC,DF⊥BC,垂足分别是E、F.
已知:如图,△ABC中,AC=6,BC=8,AB=10,∠BCA的平分线与AB边的垂直平分线相交于点D,DE⊥AC,DF⊥BC,垂足分别是E、F.