题目内容
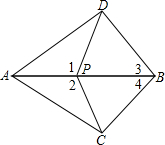 如图,点P在AB上,∠1=∠2,∠3=∠4,求证:PC=PD.
如图,点P在AB上,∠1=∠2,∠3=∠4,求证:PC=PD.
证明:∵∠1+∠DPB=180°,∠2+∠CPB=180°,∠1=∠2,
∴∠DPB=∠CPB,
∵在△BDP和△BCP中,
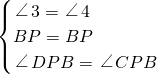 ,
,
∴△BDP≌△BCP(ASA),
∴PD=PC.
分析:由等角的补角相等得到一对角相等,再由已知的一对角相等及公共边PB,利用ASA得到三角形BDP与三角形BCP全等,由全等三角形的对应边相等即可得证.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.
∴∠DPB=∠CPB,
∵在△BDP和△BCP中,
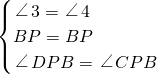 ,
,∴△BDP≌△BCP(ASA),
∴PD=PC.
分析:由等角的补角相等得到一对角相等,再由已知的一对角相等及公共边PB,利用ASA得到三角形BDP与三角形BCP全等,由全等三角形的对应边相等即可得证.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
 12、如图,点E在AB上,AC=AD,请你添加一个条件,使图中存在全等三角形,所添条件为
12、如图,点E在AB上,AC=AD,请你添加一个条件,使图中存在全等三角形,所添条件为 20、如图,点P在AB上,∠1=∠2,∠3=∠4,求证:AC=AD.
20、如图,点P在AB上,∠1=∠2,∠3=∠4,求证:AC=AD. 已知:如图,点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C.
已知:如图,点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C. 24、如图,点E在AB上,AD=AC,∠DAB=∠CAB.写出图中所有全等三角形
24、如图,点E在AB上,AD=AC,∠DAB=∠CAB.写出图中所有全等三角形 如图,点D在AB上,直线DG交AF于点E.请从①DG∥AC,②AF平分∠BAC,③AD=DE中任选两个作为条件,余下一个作为结论,构造一个真命题,并说明理由.已知:
如图,点D在AB上,直线DG交AF于点E.请从①DG∥AC,②AF平分∠BAC,③AD=DE中任选两个作为条件,余下一个作为结论,构造一个真命题,并说明理由.已知: