题目内容
 已知:如图是两个有重叠的直角三角形,可以看作是将其中的一个直角三角形ABC沿着BC方向平移BE距离得到另一直角三角形DEF,其中AB=8,BE=5,DH=3,求四边形DHCF的面积.
已知:如图是两个有重叠的直角三角形,可以看作是将其中的一个直角三角形ABC沿着BC方向平移BE距离得到另一直角三角形DEF,其中AB=8,BE=5,DH=3,求四边形DHCF的面积.
解:由平移的性质可得:AB∥DE,AB=DE,△ABC≌△DEF,
∴△CEH∽△CBA,
∴ ,
,
∵AB=8,BE=5,DH=3,
∴EH=DE-DH=8-3=5,BC=CE+BE=CE+5,
∴ ,
,
解得:CE= ,
,
∴BC=BE+CE= ,
,
∴S四边形DHCF=S△DEF-S△ECH=S△ABC-S△ECH= AB•BC-
AB•BC- CE•EH=
CE•EH= ×8×
×8× -
- ×
× ×5=
×5= .
.
分析:首先由平移的性质可得:AB∥DE,AB=DE,△ABC≌△DEF,可得△CEH∽△CBA,然后由相似三角形的对应边成比例,可求得CE的长,继而由S四边形DHCF=S△DEF-S△ECH=S△ABC-S△ECH,求得四边形DHCF的面积.
点评:此题考查了相似三角形的判定与性质以及平移的性质.此题难度适中,注意掌握数形结合思想的应用,注意掌握平移中的对应关系.
∴△CEH∽△CBA,
∴
 ,
,∵AB=8,BE=5,DH=3,
∴EH=DE-DH=8-3=5,BC=CE+BE=CE+5,
∴
 ,
,解得:CE=
 ,
,∴BC=BE+CE=
 ,
,∴S四边形DHCF=S△DEF-S△ECH=S△ABC-S△ECH=
 AB•BC-
AB•BC- CE•EH=
CE•EH= ×8×
×8× -
- ×
× ×5=
×5= .
.分析:首先由平移的性质可得:AB∥DE,AB=DE,△ABC≌△DEF,可得△CEH∽△CBA,然后由相似三角形的对应边成比例,可求得CE的长,继而由S四边形DHCF=S△DEF-S△ECH=S△ABC-S△ECH,求得四边形DHCF的面积.
点评:此题考查了相似三角形的判定与性质以及平移的性质.此题难度适中,注意掌握数形结合思想的应用,注意掌握平移中的对应关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
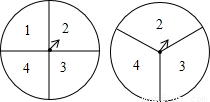
 内标上数字,如图所示.游戏规定,转动两个转盘停止后,指针必须指到某一数字,否则重转.
内标上数字,如图所示.游戏规定,转动两个转盘停止后,指针必须指到某一数字,否则重转. 内标上数字,如图所示.游戏规定,转动两个转盘停止后,指针必须指到某一数字,否则重转.
内标上数字,如图所示.游戏规定,转动两个转盘停止后,指针必须指到某一数字,否则重转.