题目内容
(1)已知关于x的方程(m2-1)x2-3(3m-1)x+18=0有两个正整数根(m是整数),试求方程的解.
(2)甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份 内标上数字,如图所示.游戏规定,转动两个转盘停止后,指针必须指到某一数字,否则重转.
内标上数字,如图所示.游戏规定,转动两个转盘停止后,指针必须指到某一数字,否则重转.
(a)请用树状图或列表法列出所有可能的结果;
(b)若指针所指的两个数字都是(1)中方程的解时,则甲获胜;若指针所指的两个数字都不是(1)中方程的解时,则乙获胜,问他们两人谁获胜的概率大?请分析说明.
解:(1)∵方程有两个实数根,
∴m2-1≠0,
∵(m2-1)x2-3(3m-1)x+18=0,
∴[(m+1)x-6][(m-1)x-3]=0,
解得:x1= ,x2=
,x2=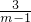 ,
,
∵关于x的方程(m2-1)x2-3(3m-1)x+18=0有两个正整数根(m是整数),
∴ ,
,
即 ,
,
∴m=2,
∴原方程的解为:x1=2,x2=3;
(2)(a)列表得:
则共有12种等可能的结果;
(b)乙获胜的概率大.
理由:由(a)得:P(甲获胜)= ,P(乙获胜)=1-
,P(乙获胜)=1- =
= ,
,
故乙获胜的概率大.
分析:(1)由方程有两个实数根,可得m2-1≠0,然后利用因式分解法解此方程,又由关于x的方程(m2-1)x2-3(3m-1)x+18=0有两个正整数根(m是整数),即可求得m的值,继而求得答案;
(2)(a)首先根据题意画出表格,然后由表格即可求得所有等可能的结果;
(b)由(a)中的表格,即可求得甲获胜与乙获胜的概率,继而可求得答案.
点评:此题考查了一元二次方程的解法以及列表法与树状图法求概率.注意概率=所求情况数与总情况数之比;注意分类讨论思想的应用.
∴m2-1≠0,
∵(m2-1)x2-3(3m-1)x+18=0,
∴[(m+1)x-6][(m-1)x-3]=0,
解得:x1=
 ,x2=
,x2=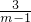 ,
,∵关于x的方程(m2-1)x2-3(3m-1)x+18=0有两个正整数根(m是整数),
∴
 ,
,即
 ,
,∴m=2,
∴原方程的解为:x1=2,x2=3;
(2)(a)列表得:
| 1 | 2 | 3 | 4 | |
| 2 | 1,2 | 2,2 | 3,2 | 4,2 |
| 3 | 1,3 | 2,3 | 3,3 | 4,3 |
| 4 | 1,4 | 2,4 | 3,4 | 4,4 |
(b)乙获胜的概率大.
理由:由(a)得:P(甲获胜)=
 ,P(乙获胜)=1-
,P(乙获胜)=1- =
= ,
,故乙获胜的概率大.
分析:(1)由方程有两个实数根,可得m2-1≠0,然后利用因式分解法解此方程,又由关于x的方程(m2-1)x2-3(3m-1)x+18=0有两个正整数根(m是整数),即可求得m的值,继而求得答案;
(2)(a)首先根据题意画出表格,然后由表格即可求得所有等可能的结果;
(b)由(a)中的表格,即可求得甲获胜与乙获胜的概率,继而可求得答案.
点评:此题考查了一元二次方程的解法以及列表法与树状图法求概率.注意概率=所求情况数与总情况数之比;注意分类讨论思想的应用.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
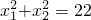 ,求m的值.
,求m的值.