题目内容
定义:可以表示为两个互质整数的商的形式的数称为有理数,整数可以看作分母为1的有理数;反之为无理数.如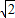 不能表示为两个互质的整数的商,所以,
不能表示为两个互质的整数的商,所以,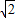 是无理数.
是无理数.可以这样证明:
设
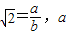 与b 是互质的两个整数,且b≠0.
与b 是互质的两个整数,且b≠0.则
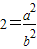 a2=2b2因为b是整数且不为0,所以,a是不为0的偶数,设a=2n,(n是整数),所以b2=2n2,所以b也是偶数,与a,b是互质的正整数矛盾.所以,
a2=2b2因为b是整数且不为0,所以,a是不为0的偶数,设a=2n,(n是整数),所以b2=2n2,所以b也是偶数,与a,b是互质的正整数矛盾.所以,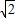 是无理数.仔细阅读上文,然后,请证明:
是无理数.仔细阅读上文,然后,请证明: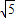 是无理数.
是无理数.
【答案】分析:先设 =
= ,再由已知条件得出
,再由已知条件得出 ,a2=5b2,又知道b是整数且不为0,所以a不为0且为5的倍数,再设a=5n,(n是整数),
,a2=5b2,又知道b是整数且不为0,所以a不为0且为5的倍数,再设a=5n,(n是整数),
则b2=5n2,从而得到b也为5的倍数,与a,b是互质的正整数矛盾,从而证明了答案.
解答:解:设 与b是互质的两个整数,且b≠0.则
与b是互质的两个整数,且b≠0.则 ,a2=5b2,
,a2=5b2,
因为b是整数且不为0,
所以a不为0且为5的倍数,设a=5n,(n是整数),
所以b2=5n2,
所以b也为5的倍数,
与a,b是互质的正整数矛盾.
所以 是无理数.
是无理数.
点评:本题考查了无理数的概念,解题的关键是根据所给事例模仿去做,做到举一反三.
 =
= ,再由已知条件得出
,再由已知条件得出 ,a2=5b2,又知道b是整数且不为0,所以a不为0且为5的倍数,再设a=5n,(n是整数),
,a2=5b2,又知道b是整数且不为0,所以a不为0且为5的倍数,再设a=5n,(n是整数),则b2=5n2,从而得到b也为5的倍数,与a,b是互质的正整数矛盾,从而证明了答案.
解答:解:设
 与b是互质的两个整数,且b≠0.则
与b是互质的两个整数,且b≠0.则 ,a2=5b2,
,a2=5b2,因为b是整数且不为0,
所以a不为0且为5的倍数,设a=5n,(n是整数),
所以b2=5n2,
所以b也为5的倍数,
与a,b是互质的正整数矛盾.
所以
 是无理数.
是无理数.点评:本题考查了无理数的概念,解题的关键是根据所给事例模仿去做,做到举一反三.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
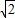 不能表示为两个互质的整数的商,所以,
不能表示为两个互质的整数的商,所以,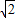 是无理数.
是无理数.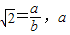 与b 是互质的两个整数,且b≠0.
与b 是互质的两个整数,且b≠0.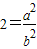 a2=2b2因为b是整数且不为0,所以,a是不为0的偶数,设a=2n,(n是整数),所以b2=2n2,所以b也是偶数,与a,b是互质的正整数矛盾.所以,
a2=2b2因为b是整数且不为0,所以,a是不为0的偶数,设a=2n,(n是整数),所以b2=2n2,所以b也是偶数,与a,b是互质的正整数矛盾.所以,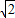 是无理数.仔细阅读上文,然后,请证明:
是无理数.仔细阅读上文,然后,请证明: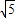 是无理数.
是无理数.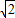 不能表示为两个互质的整数的商,所以,
不能表示为两个互质的整数的商,所以,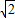 是无理数.
是无理数.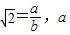 与b 是互质的两个整数,且b≠0.
与b 是互质的两个整数,且b≠0.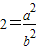 a2=2b2因为b是整数且不为0,所以,a是不为0的偶数,设a=2n,(n是整数),所以b2=2n2,所以b也是偶数,与a,b是互质的正整数矛盾.所以,
a2=2b2因为b是整数且不为0,所以,a是不为0的偶数,设a=2n,(n是整数),所以b2=2n2,所以b也是偶数,与a,b是互质的正整数矛盾.所以,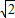 是无理数.仔细阅读上文,然后,请证明:
是无理数.仔细阅读上文,然后,请证明: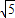 是无理数.
是无理数.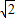 不能表示为两个互质的整数的商,所以,
不能表示为两个互质的整数的商,所以,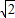 是无理数.
是无理数.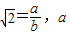 与b 是互质的两个整数,且b≠0.
与b 是互质的两个整数,且b≠0.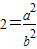 a2=2b2因为b是整数且不为0,所以,a是不为0的偶数,设a=2n,(n是整数),所以b2=2n2,所以b也是偶数,与a,b是互质的正整数矛盾.所以,
a2=2b2因为b是整数且不为0,所以,a是不为0的偶数,设a=2n,(n是整数),所以b2=2n2,所以b也是偶数,与a,b是互质的正整数矛盾.所以,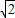 是无理数.仔细阅读上文,然后,请证明:
是无理数.仔细阅读上文,然后,请证明: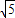 是无理数.
是无理数.