题目内容
1.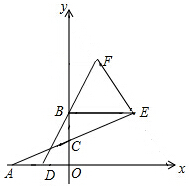 如图,A(-4,0),B(0,4),C,D分别为OB,OA的中点,E,F分别为AC,DB上一点,CE=AC,BD=BF,连接EF.
如图,A(-4,0),B(0,4),C,D分别为OB,OA的中点,E,F分别为AC,DB上一点,CE=AC,BD=BF,连接EF.(1)求直线EF的解析式;
(2)求证:EF⊥AC.
分析 (1)作EM⊥x轴于M,FG⊥y轴于G,根据平行线的性质和三角形全等的性质求出OM、EM、FG、BG的长,求出E、F的坐标,用待定系数法求出解析式;
(2)求出直线EF与x轴的交点,根据相似三角形的判定和性质证明结论.
解答 解:(1)作EM⊥x轴于M,FG⊥y轴于G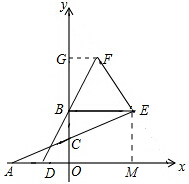 ,
,
∵A(-4,0),B(0,4),
∴OA=4,OB=4,
∵C,D分别为OB,OA的中点,
∴OD=2,OC=2,
由题意可知,EM∥OB,CE=AC,
∴EM=2OC=4,OM=OA=4,
∴点E的坐标(4,4),
∵FG∥OD,BD=BF,
∴FG=OD=2,BG=OB=4,
∴点F的坐标(2,8),
设EF的解析式为y=kx+b,
则$\left\{\begin{array}{l}{4k+b=4}\\{2k+b=8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=12}\end{array}\right.$,
∴EF的解析式为y=-2x+12.
(2)当y=0时,即=-2x+12=0,x=6,
∴点N的坐标为(-6,0),
则ON=6,
∵OA=4,OC=2,由勾股定理,AC=2$\sqrt{5}$,
$\frac{AC}{AN}$=$\frac{2\sqrt{5}}{10}$=$\frac{\sqrt{5}}{5}$,
$\frac{OA}{AE}$=$\frac{4}{4\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,
∴$\frac{AC}{AN}$=$\frac{AO}{AE}$,∠A=∠A,
∴△AOC∽△AEN,
∴∠AOC=∠AEN=90°,
∴EF⊥AC.
点评 本题考查的是一次函数的综合应用,熟练运用待定系数法求一次函数的解析式是解题的关键,两边对应成比例且夹角相等的两个三角形相似.

 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 0 | B. | -1 | C. | 0或-1 | D. | 4 |
(1)根据题意,填写下表:
| 累计购物 实际花费 | 130 | x(100<x<200) | 200 | x(200<x<300) |
| 在甲商场 | 124 | 0.8x+20 | 180 | 0.8x+20 |
| 在乙商场 | 120 | x-10 | 180 | x-20 |
 如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).
如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).