题目内容
18.设N=23x+92y为完全平方数,且N<2000,x、y为正整数,求x+y的值.分析 此题可根据N=23x+92y为完全平方数,N不超过2392,则x+4y=23m2<2000,确定出m2的取值,再分别讨论得出正整数对(x,y),再代入计算即可求解.
解答 解:N=23x+92y=23(x+4y),且23为质数,N<2000,x、y为正整数,
设x+4y=23m2(m为正整数),且N=232m2<2000,得:m2<$\frac{2000}{2{3}^{2}}$=$\frac{2000}{529}$<4,
∴m2=1,
当m2=1时,则x+4y=23,
当x=3,y=5时,x+y=8;
当x=7,y=4时,x+y=11;
当x=11,y=3时,x+y=14;
当x=15,y=2时,x+y=17;
当x=19,y=1时,x+y=20.
综上所述,x+y的值为8或11或14或17或20.
点评 本题考查了完全平方式的应用,关键是由题意确定出x+4y的值,再分别得出满足等式的整数x,y,比较复杂.

练习册系列答案
相关题目
7.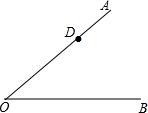 如图,已知∠AOB=40°,D为射线OA上一点,在射线OB上找一点C,使△ODC为等腰三角形,则这样的C点有( )
如图,已知∠AOB=40°,D为射线OA上一点,在射线OB上找一点C,使△ODC为等腰三角形,则这样的C点有( )
 如图,已知∠AOB=40°,D为射线OA上一点,在射线OB上找一点C,使△ODC为等腰三角形,则这样的C点有( )
如图,已知∠AOB=40°,D为射线OA上一点,在射线OB上找一点C,使△ODC为等腰三角形,则这样的C点有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
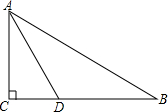 如图,在△ABC中,∠C=90°,∠B=30°,AD是∠BAC的角平分线,若AD=4,求△ABC的周长.
如图,在△ABC中,∠C=90°,∠B=30°,AD是∠BAC的角平分线,若AD=4,求△ABC的周长. 有理数a,b,c在数轴上的位置如图所示,化简|a+c|-|c-b|+2|b+a|.
有理数a,b,c在数轴上的位置如图所示,化简|a+c|-|c-b|+2|b+a|. 已知一次函数y=-$\frac{3}{4}$x+4
已知一次函数y=-$\frac{3}{4}$x+4