Question

【题目】如图1，已知二次函数y=mx2+3mx﹣m的图象与x轴交于A，B两点（点A在点B的左侧），顶点D和点B关于过点A的直线l：y=﹣x﹣对称．

（1）求A、B两点的坐标及二次函数解析式；

（2）如图2，作直线AD，过点B作AD的平行线交直线1于点E，若点P是直线AD上的一动点，点Q是直线AE上的一动点．连接DQ、QP、PE，试求DQ+QP+PE的最小值；若不存在，请说明理由：

（3）将二次函数图象向右平移个单位，再向上平移3个单位，平移后的二次函数图象上存在一点M，其横坐标为3，在y轴上是否存在点F，使得∠MAF=45°？若存在，请求出点F坐标；若不存在，请说明理由．

Answer 1

【答案】（1）A（﹣，0），B（，0）；抛物线解析式y=x2+x﹣；（2）12；（3）（0，），（0，﹣）

【解析】

（1）在y=mx2+3mx﹣m中令y=0，解方程求得x的值即可求得A、B的坐标，继而根据已知求出点D的坐标，把点D坐标代入函数解析式y=mx2+3mx﹣m利用待定系数法求得m即可得函数解析式；

（2）先求出直线AD解析式，再根据直线BE∥AD，求得直线BE解析式，继而可得点E坐标，如图2，作点P关于AE 的对称点P'，作点E关于x轴的对称点E'，根据对称性可得PQ=P'Q，PE=EP'=P'E'，从而有DQ+PQ+PE=DQ+P'Q+P'E'，可知当D，Q，E'三点共线时，DQ+PQ+PE值最小，即DQ+PQ+PE最小值为DE'，根据D、E'坐标即可求得答案；

（3）分情况进行讨论即可得答案.

（1）∵令y=0，

∴0=m x2+3mx﹣m，

∴x1=，x2=﹣，

∴A（﹣，0），B（，0），

∴顶点D的横坐标为﹣，

∵直线y=﹣x﹣ 与x轴所成锐角为30°，且D，B关于y=﹣x﹣对称，

∴∠DAB=60°，且D点横坐标为﹣，

∴D（﹣，﹣3），

∴﹣3=m﹣m﹣m，

∴m=，

∴抛物线解析式y=x2+x﹣；

（2）∵A（﹣，0），D（﹣，﹣3），

∴直线AD解析式y=﹣x﹣，

∵直线BE∥AD，

∴直线BE解析式y=﹣x+，

∴﹣x﹣=﹣x+，

∴x=，

∴E（，﹣3），

如图2，作点P关于AE 的对称点P'，作点E关于x轴的对称点E'，

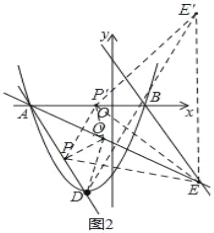
根据对称性可得PQ=P'Q，PE=EP'=P'E'，

∴DQ+PQ+PE=DQ+P'Q+P'E'，

∴当D，Q，E'三点共线时，DQ+PQ+PE值最小，

即DQ+PQ+PE最小值为DE'，

∵D（﹣，﹣3），E'（，3），

∴DE'=12，

∴DQ+PQ+PE最小值为12；

（3）∵抛物线y=（x+）2﹣3图象向右平移个单位，再向上平移3个单位，

∴平移后解析式y=x2，

当x=3时，y=3，

∴M （3，3），

如图3

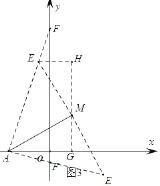
若以AM为直角边，点M是直角顶点，在AM上方作等腰直角△AME，则∠EAM=45°，

直线AE交y轴于F点，作MG⊥x轴，EH⊥MG，则△EHM≌△AMG，

∵A（﹣，0），M（3，3），

∴E（3﹣3，3+），

∴直线AE解析式：y=x+，

∴F（0，），

若以AM为直角边，点M是直角顶点，在AM上方作等腰直角△AME，

同理可得：F（0，﹣）.