Question

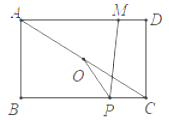
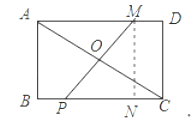
【题目】如图，在矩形ABCD中，AB＝4，AD＝5，连接AC，O是AC的中点，M是AD上一点，且MD＝1，P是BC上一动点，则PM﹣PO的最大值为_____．

Answer 1

【答案】

【解析】

连接MO并延长交BC于P，则此时，PMPO的值最大，且PMPO的最大值＝OM，根据全等三角形的性质得到AM＝CP＝4，OM＝OP，求得PB＝1，过M作MN⊥BC于N，得到四边形MNCD是矩形，得到MN＝CD，CN＝DM，根据勾股定理即可得到结论．

∵在矩形ABCD中，AD＝5，MD＝1，

∴AM＝AD﹣DM＝5﹣1＝4，

连接MO并延长交BC于P，

则此时，PM﹣PO的值最大，且PM﹣PO的最大值＝OM，

∵AM∥CP，

∴∠MAO＝∠PCO，

∵∠AOM＝∠COP，AO＝CO，

∴△AOM≌△COP（ASA），

∴AM＝CP＝4，OM＝OP，

∴PB＝5﹣4＝1，

过M作MN⊥BC于N，

∴四边形MNCD是矩形，

∴MN＝CD＝AB＝4，CN＝DM＝1，

∴PN＝5﹣1﹣1＝3，

∴MP＝，

∴OM＝＝．

故答案为．