Question

【题目】如图1,AB∥CD,∠BAD,∠ADC 的平分线AE,DE相交于点E.

(1)证明:AE⊥DE;

(2)如图2,过点E作直线AB,AD,DC的垂线,垂足分别为F,G,H,证明:EF=EG=EH;

(3)如图3,过点E的直线与AB,DC分别相交于点B,C(B、C在AD的同侧)

①求证: E为线段BC的中点;

②若S△ADE=8, S△ABE=2,求△CDE的面积.

Answer 1

【答案】（1）见详解；（2）见详解；（3）①见详解；②6

【解析】

（1）由AB∥CD，可知,再由角平分线的定义可得,由三角形内角和可得,则结论可证；

（2）由角平分线的性质即可证明EF=EG=EH；

（3）①过点E作EF⊥AB交AB的延长线于点F，EG⊥CD交CD于点G，由第（2）问中可知EF=EG，则可利用ASA证明,则,则结论可证；

②通过计算可知，则△CDE的面积可求.

（1）证明：∵AB∥CD

∴

∵AE平分，DE平分，

∴

∴

∴

∴AE⊥DE

（2）∵AE平分，

∴

∵DE平分，

∴

∴

（3）①过点E作EF⊥AB交AB的延长线于点F，EG⊥CD交CD于点G，

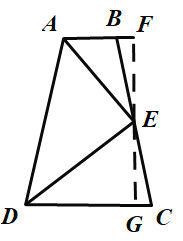
由（2）可知

∵EF⊥AB，EG⊥CD

∴

在和中，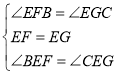

∴

∴

∴E为线段BC的中点

②∵

∴

∵

∴

∴