题目内容
已知在△ABC中，点D是AB边上的一点，点F是BC边延长线上的一点，连接DF交AC于E，且AD=CF，求证：
=
．
| BF |
| BD |
| AE |
| CE |
考点：相似三角形的判定与性质
专题：证明题
分析：过点C作CG平行AB，在△BDF和△CGF、△ECG和△EAD中分别可得到线段的比例，进一步可得结论．
解答：
证明：过点C作CG∥AB交DE于点G，
在△BDF和△CGF中，
∵CG∥AB，
∴
=
，即
=
，
在△ECG和△EAD中，同理可得：
=
，
又∵AD=CF，
∴
=
．
证明：过点C作CG∥AB交DE于点G，在△BDF和△CGF中，
∵CG∥AB，
∴
| BF |
| CF |
| BD |
| CG |
| BF |
| BD |
| CF |
| CG |
在△ECG和△EAD中，同理可得：
| AD |
| CG |
| AE |
| CE |
又∵AD=CF，
∴
| BF |
| BD |
| AE |
| CE |
点评：本题主要考查平行线分线段成比例性质的应用，解题的关键是作出平行，找到线段之间的关系．
练习册系列答案
相关题目
已知不等式组
无解，则a的取值范围是（ ）
|
| A、a＞1 | B、a＜1 |
| C、a≤1 | D、a≥1 |
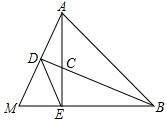如图所示，AE、BD是△ABM的高，AE、BD交于点C，且AE=BE，BD平分∠ABM．
