题目内容
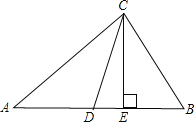
【题目】如图,△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠A=40°,∠B=72°.
(1)求∠DCE的度数;
(2)试写出∠DCE与∠A、∠B的之间的关系式.(不必证明)
【答案】(1)∠DCE=16°;(2)∠DCE=![]() (∠B-∠A).
(∠B-∠A).
【解析】
(1)由CD是∠ACB的角平分线,求出∠DCB 的度数,再由CE是AB边上的高,求出∠ECB,相减即可求出∠DCE度数,
(2)证明过程与上一问思路相同.
解:(1)∵∠A=40°,∠B=72°,
∴∠ACB=68°
∵CD平分∠ACB
∴∠DCB=![]() ∠ACB=34°
∠ACB=34°
∵CE是AB边上的高
∴∠ECB=90°-∠B=90°-72°=18°
∴∠DCE=34°-18°=16°
(2)∠DCE=![]() (∠B-∠A).
(∠B-∠A).

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
【题目】七年级(3)班学生参加学校组织的“绿色奥运”知识竞赛,老师将学生的成绩按10分的组距分段,统计每个分数段出现的频数,填入频数统计表,并绘制频数直方图.
七(3)班“绿色奥运”知识竞赛成绩频数统计表
分数段/分 | 组中值/分 | 频数/人 | 频率 |
49.5~59.5 | 54.5 | a | 0.050 |
59.5~69.5 | 64.5 | 9 | 0.225 |
69.5~79.5 | 74.5 | 10 | 0.250 |
79.5~89.5 | 84.5 | 14 | 0.350 |
89.5~99.5 | 94.5 | 5 | b |
七(3)班“绿色奥运”知识竞赛成绩频数直方图
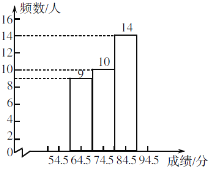
(1)频数统计表中a=_____,b=______;
(2)把频数直方图补充完整;
(3)学校设定成绩在69.5分以上的学生将获得一等奖或二等奖,一等奖奖励作业本15本及奖金50元,二等奖奖励作业本10本及奖金30元. 已知这部分学生共获得作业本335本,请你求出他们共获得的奖金.