题目内容
如图,已知二次函数y=ax2+2x+c(a>0)图象的顶点M在反比例函数 上,且与x轴交于AB两点.
上,且与x轴交于AB两点.(1)若二次函数的对称轴为
 ,试求a,c的值;
,试求a,c的值;(2)在(1)的条件下求AB的长;
(3)若二次函数的对称轴与x轴的交点为N,当NO+MN取最小值时,试求二次函数的解析式.

【答案】分析:(1)根据对称轴x=- =-
=- ,求得二次函数y=ax2+2x+c(a>0)中的a,再根据顶点在反比例函数
,求得二次函数y=ax2+2x+c(a>0)中的a,再根据顶点在反比例函数 上,求出c即可;
上,求出c即可;
(2)求得抛物线与x轴的交点坐标,再用点B的横坐标减去点A的横坐标即可.
(3)可用含有a的式子表示点M、N的坐标,即求出a的值,再求得解析式.
解答:解:(1)∵二次函数的对称轴为 ,
,
∴- =-
=- ,
,
解得a=2,
∵二次函数y=ax2+2x+c(a>0)图象的顶点M在反比例函数 上,
上,
∴顶点为(- ,c-
,c- ),
),
∴ (c-
(c- )=-3,
)=-3,
解得c=- ,
,
∴二次函数的解析式为y=2x2+2x- ;
;
(2)∵二次函数的解析式为y=2x2+2x- ;
;
∴令y=0,2x2+2x- =0;
=0;
解得x= .
.
∴AB= =2
=2 ;
;
(3)根据对称轴x=- ,当x=-
,当x=- 时,y=-3a,
时,y=-3a,
∴NO+MN= +3a≥2
+3a≥2 =2
=2 ,当3a=
,当3a= 时NO+MN最小,
时NO+MN最小,
即3a2=1时,a= ,
,
∴c=0,
∴此时二次函数的解析式为y= x2+2x.
x2+2x.
点评:本题是二次函数的综合题,其中涉及到的知识点有最值问题和两点之间的距离等知识点,是各地中考的热点和难点,解题时注意数形结合等数学思想的运用,同学们要加强训练,属于中档题.
 =-
=- ,求得二次函数y=ax2+2x+c(a>0)中的a,再根据顶点在反比例函数
,求得二次函数y=ax2+2x+c(a>0)中的a,再根据顶点在反比例函数 上,求出c即可;
上,求出c即可;(2)求得抛物线与x轴的交点坐标,再用点B的横坐标减去点A的横坐标即可.
(3)可用含有a的式子表示点M、N的坐标,即求出a的值,再求得解析式.
解答:解:(1)∵二次函数的对称轴为
 ,
,∴-
 =-
=- ,
,解得a=2,
∵二次函数y=ax2+2x+c(a>0)图象的顶点M在反比例函数
 上,
上,∴顶点为(-
 ,c-
,c- ),
),∴
 (c-
(c- )=-3,
)=-3,解得c=-
 ,
,∴二次函数的解析式为y=2x2+2x-
 ;
;(2)∵二次函数的解析式为y=2x2+2x-
 ;
;∴令y=0,2x2+2x-
 =0;
=0;解得x=
 .
.∴AB=
 =2
=2 ;
;(3)根据对称轴x=-
 ,当x=-
,当x=- 时,y=-3a,
时,y=-3a,∴NO+MN=
 +3a≥2
+3a≥2 =2
=2 ,当3a=
,当3a= 时NO+MN最小,
时NO+MN最小,即3a2=1时,a=
 ,
,∴c=0,
∴此时二次函数的解析式为y=
 x2+2x.
x2+2x.点评:本题是二次函数的综合题,其中涉及到的知识点有最值问题和两点之间的距离等知识点,是各地中考的热点和难点,解题时注意数形结合等数学思想的运用,同学们要加强训练,属于中档题.

练习册系列答案
相关题目
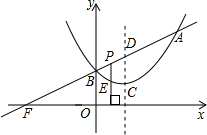 三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.
三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.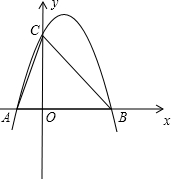
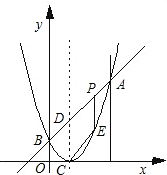 如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.
如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.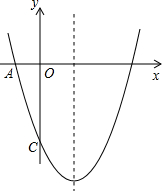 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).
如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).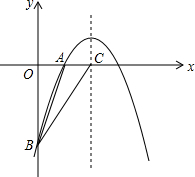 (2012•衡水一模)如图,已知二次函数
(2012•衡水一模)如图,已知二次函数