题目内容
如图，已知E是边长为12的正方形的边AB上一点，且AE=5，P是对角线AC上任意一点，则PE+PB的最小值是________．
13
分析：由正方形性质的得出B、D关于AC对称，根据两点之间线段最短可知，连接DE，交AC于P，连接BP，则此时PB+PE的值最小．
解答：
解：如图，连接DE，交AC于P，连接BP，则此时PB+PE的值最小．
∵四边形ABCD是正方形，
∴B、D关于AC对称，
∴PB=PD，
∴PB+PE=PD+PE=DE，
∵E是边长为12的正方形的边AB上一点，且AE=5，
∴PB+PE的值最小为：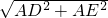
=
=13．
故答案为：13．
点评：本题考查了轴对称-最短路线问题，正方形的性质，解此题通常是利用两点之间，线段最短的性质．
分析：由正方形性质的得出B、D关于AC对称，根据两点之间线段最短可知，连接DE，交AC于P，连接BP，则此时PB+PE的值最小．
解答：
解：如图，连接DE，交AC于P，连接BP，则此时PB+PE的值最小．∵四边形ABCD是正方形，
∴B、D关于AC对称，
∴PB=PD，
∴PB+PE=PD+PE=DE，
∵E是边长为12的正方形的边AB上一点，且AE=5，
∴PB+PE的值最小为：
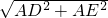==13．故答案为：13．
点评：本题考查了轴对称-最短路线问题，正方形的性质，解此题通常是利用两点之间，线段最短的性质．
练习册系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
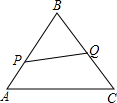匀速运动，其中点P运动的速度是1cm/s，点Q运动的速度是2cm/s，当点Q运动到点C时，P，Q都停止运动．
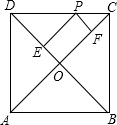如图，已知P是边长为2的正方形ABCD的边CD任意一点，且PE⊥DB，垂足为E，PF⊥CA垂足为F，则PE+PF的长是
的坐标为（-1，0）．
A的坐标为（-1，0）．
如图，已知△ABC是边长为2