题目内容
如图，⊙
的直径
是
，过
点的直线
是⊙的切线，
、
是⊙上的两点，连接
、
、
和
．
(1)求证：
；
(2)若
是
的平分线，且
，求的长．
【答案】
(1)证明: ∵
是⊙
的直径
∴
∵
切⊙于点
∴
∴
∵
∴
.
(2) 如右图,连接
,过点作
于点
.
∵
平分
∴
∴弧
弧
∵是⊙的直径
∴
又∵
∴
∵
∴
∵
∴
∴
.
【解析】（1）由AB为⊙O的直径，得：∠ADB=90°，根据MN是⊙O的切线，可知：∠AMN=90°，根据同弧所对的圆周角相等，可知：∠ADC=∠ABC，从而证得：∠CBN=∠CDB；
（2）连接OD、OC，过点O作OE⊥CD于点E，根据圆周角定理，可求得∠BOC和∠DOB的度数，故可知：∠COD的度数，在等腰△OCD中，可将CD的长求出．
练习册系列答案
相关题目
C，交BA、BC的延长线于点E、F．
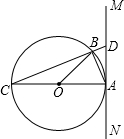如图，⊙O的直径AC=13，弦BC=12．过点A作直线MN，使∠BAM=
（1997•江西）如图，⊙O的直径AB=10，P是OA上一点，弦MN过点P，且AP=2，MP=2
如图，⊙O的直径AB=4，C为圆周上一点，AC=2，过点C作⊙O的切线DC，P点为优弧CBA上一点（不与A、C重合）