题目内容
8.点A,点B的坐标分别是(0,1),(a,b),将线段AB绕点A逆时针旋转90°后得到线段AC,则点C的坐标为( )| A. | (-b,a) | B. | (-a,b) | C. | (1-b,a+1) | D. | (-1,-b+2) |
分析 作出草图,过点B作BD⊥y轴于D,过点C作CE⊥y轴于E,根据点A、B的坐标表示出BD、AD,再求出△ABD和△CAE全等,根据全等三角形对应边相等可得CE=AD,AE=BD,然后表示出OE,再写出点C的坐标即可.
解答 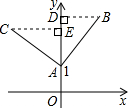 解:如图,过点B作BD⊥y轴于D,过点C作CE⊥y轴于E,
解:如图,过点B作BD⊥y轴于D,过点C作CE⊥y轴于E,
∵点A,点B的坐标分别是(0,1),(a,b),
∴BD=a,AD=b-1,
∵线段AB绕点A逆时针旋转90°后得到线段AC,
∴∠CAE+∠BAD=90°,AB=AC,
又∵∠CAE+∠C=90°,
∴∠C=∠BAD,
在△ABD和△CAE中,$\left\{\begin{array}{l}{∠C=∠BAD}\\{∠AEC=∠BDA=90°}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△CAE(AAS),
∴CE=AD=b-1,AE=BD=a,
∴OE=OA+AE=1+a,
∴点C的坐标为(1-b,a+1).
故选C.
点评 本题考查了坐标与图形性质-旋转,主要利用了全等三角形的性质,作出图形,利用数形结合的思想求解更形象直观.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
18. 如图,数轴上标出的点中任意相邻两点间的距离都相等,则a的值为( )
如图,数轴上标出的点中任意相邻两点间的距离都相等,则a的值为( )
 如图,数轴上标出的点中任意相邻两点间的距离都相等,则a的值为( )
如图,数轴上标出的点中任意相邻两点间的距离都相等,则a的值为( )| A. | 0 | B. | 2 | C. | 4 | D. | 10 |
16.用一个平面去截一个几何体,截面是三角形,这个几何体不可能是( )
| A. | 棱柱 | B. | 圆柱 | C. | 圆锥 | D. | 棱锥 |
3.如图正方形中由阴影部分组成的图形,是轴对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.下列各数:-(+3),|-4|,+6,-(-1.5)中,负数的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |