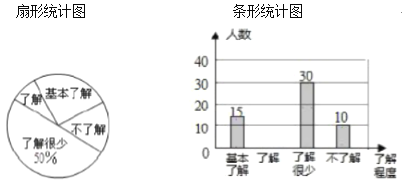
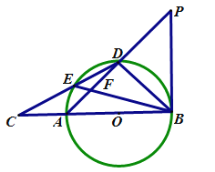
题目内容
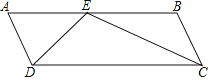
【题目】如图，
是
的直径，点
是劣弧
上一点，
，且
，
平分
，与交于点
．
（1）求证：
是的切线；
（2）若
，求
的长；
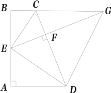
（3）延长
，
交于点
，若
，求的半径．
【答案】（1）详见解析；（2）
；（3）
【解析】
（1）由圆周角定理可得∠ADB=90°，进而可得∠DAB+∠ABD=90°，再利用等量代换得到∠DAB=∠PBD，证得∠ABP=90°即可；
（2）连接AE，由圆周角定理可得∠AEB=90°，再由角平分线的定义得到∠ABE=∠DBE，最后根据三角函数的定义即可得解答；
（3）连接OE，设
的半径为
，由等腰三角形的性质可得∠ABE=∠OEB，再由等量代换得到∠DBE=∠OEB，最后根据相似三角形的性质得到解答即可．
证明（1）∵
是的直径
∴
∴
∵
∴
∵
∴
∴
即
∴
又
是的半径
∴
是的切线
解（2）连接
∴
∵
平分
∴
∴
∴
∴
∴
∴
∴
（3）连接
，设的半径为
∴
∴
∵
∴
∴
∴
∴
∵
∴
∴
即
∴
∴
∵
∴
∵
∴
∴
即
∴
∴的半径为
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
