Question

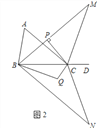
【题目】如图1，在Rt△ABC中，AC=8cm，BC=6cm，D、E分别为边AB、BC的中点，连结DE，点P从点A出发，沿折线AD﹣DE运动，到点E停止，点P在AD上以5cm/s的速度运动，在DE上以1cm/s的速度运动，过点P作PQ⊥AC于点Q，以PQ为边作正方形PQMN．设点P的运动时间为t（s）．

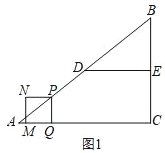
（1）当点P在线段DE上运动时，线段DP的长为_____cm．（用含t的代数式表示）

（2）当正方形PQMN与△ABC重叠部分图形为五边形时，设五边形的面积为S（cm2），求S与t的函数关系式，并写出t的取值范围．

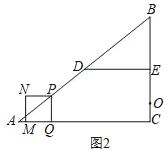
（3）如图2，若点O在线段BC上，且CO=1，以点O为圆心，1cm长为半径作圆，当点P开始运动时，⊙O的半径以0.2cm/s的速度开始不断增大，当⊙O与正方形PQMN的边所在直线相切时，求此时的t值．

Answer 1

【答案】（1）t﹣1；（2）S=﹣t2+3t+3（1＜t＜4）；（3）t=s．

【解析】分析：（1）根据勾股定理求出AB，根据D为AB中点，求出AD，根据点P在AD上的速度，即可求出点P在AD段的运动时间，再求出点P在DP段的运动时间，最后根据DE段运动速度为1cm/s，即可求出DP；

（2）由正方形PQMN与△ABC重叠部分图形为五边形，可知点P在DE上，求出DP=t﹣1，PQ=3，根据MN∥BC，求出FN的长，从而得到FM的长，再根据S=S梯形FMHD+S矩形DHQP，列出S与t的函数关系式即可；

（3）当圆与边PQ相切时，可求得r=PE=5﹣t，然后由r以0.2cm/s的速度不断增大，r=1+0.2t，然后列方程求解即可；当圆与MN相切时，r=CM=8﹣t=1+0.2t，从而可求得t的值．

详解：（1）由勾股定理可知：AB==10．

∵D、E分别为AB和BC的中点，

∴DE=AC=4，AD=AB=5，

∴点P在AD上的运动时间==1s，当点P在线段DE上运动时，DP段的运动时间为（t﹣1）s．

∵DE段运动速度为1cm/s，∴DP=（t﹣1）cm．

故答案为：t﹣1．

（2）当正方形PQMN与△ABC重叠部分图形为五边形时，有一种情况，如下图所示．

当正方形的边长大于DP时，重叠部分为五边形，

∴3＞t﹣1，t＜4，DP＞0，∴t﹣1＞0，

解得：t＞1，∴1＜t＜4．

∵△DFN∽△ABC，∴===．

∵DN=PN﹣PD，∴DN=3﹣（t﹣1）=4﹣t，

∴=，∴FN=，

∴FM=3﹣=，

S=S梯形FMHD+S矩形DHQP，

∴S=×（+3）×（4﹣t）+3（t﹣1）=﹣t2+3t+3（1＜t＜4）．

（3）①当圆与边PQ相切时，如图：

当圆与PQ相切时，r=PE，由（1）可知，PD=（t﹣1）cm，

∴PE=DE﹣DP=4﹣（t﹣1）=（5﹣t）cm．

∵r以0.2cm/s的速度不断增大，∴r=1+0.2t，

∴1+0.2t=5﹣t，解得：t=s．

②当圆与MN相切时，r=CM．

由（1）可知，DP=（t﹣1）cm，则PE=CQ=（5﹣t）cm，MQ=3cm，

∴MC=MQ+CQ=5﹣t+3=（8﹣t）cm，

∴1+0.2t=8﹣t，解得：t=s．

∵P到E点停止，∴t﹣1≤4，即t≤5，∴t=s（舍）．

综上所述：当t=s时，⊙O与正方形PQMN的边所在直线相切．